如图,点P(-3,1)是反比例函数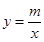 的图象上的一点.
的图象上的一点.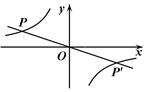
求该反比例函数的解析式;
设直线
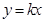 与双曲线
与双曲线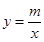 的两个交点分别为P和P′,
的两个交点分别为P和P′,
当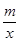 <
<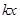 时,直接写出x的取值范围.
时,直接写出x的取值范围.
中日钓鱼岛争端持续,我海监船加大钓鱼岛海域的巡航维权力度.如图,OA⊥OB,OA=45海里,OB=15海里,钓鱼岛位于O点,我国海监船在点B处发现有一不明国籍的渔船,自A点出发沿着AO方向匀速驶向钓鱼岛所在地点O,我国海监船立即从B处出发以相同的速度沿某直线去拦截这艘渔船,结果在点C处截住了渔船.
(1)请用直尺和圆规作出C处的位置;
(2)求我国海监船行驶的航程BC的长.
如图,已知点A、F、E、C在同一直线上,AB∥CD,∠ABE=∠CDF,AF=CE.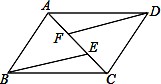
(1)从图中任找两组全等三角形;
(2)从(1)中任选一组进行证明.
在3×3的正方形格点图中,有格点△ABC和△DEF,且△ABC和△DEF关于某直线成轴对称,请在备用图中画出4个这样的△DEF(不能重复).
已知5a+2的立方根是3,3a+b-1的算术平方根是4,c是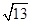 的整数部分,
的整数部分,
求3a-b+c的平方根.
问题解决
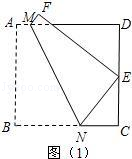
(1)如图(1),将正方形纸片ABCD折叠,使点B落在CD边上一点E(不与点C,D重合),压平后得到折痕MN.当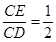 时,求
时,求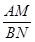 的值.
的值.
类比归纳
(2)在图(1)中,若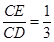 则
则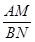 的值等于;若
的值等于;若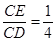 则
则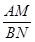 的值等于;若
的值等于;若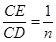 (
(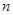 为整数),则
为整数),则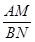 的值等于.(用含
的值等于.(用含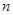 的式子表示)
的式子表示)
联系拓广
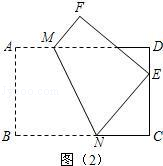
(3)如图(2),将矩形纸片ABCD折叠,使点B落在CD边上一点E(不与点C,D重合),压平后得到折痕MN,设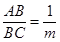 (
(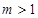 ),
),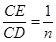 ,则
,则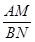 的值等于.
的值等于.
(用含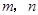 的式子表示)
的式子表示)