如图，D是△ABC中AB边的中点，△BCE和△ACF都是等边三角形， M、N分别是CE、CF的中点.
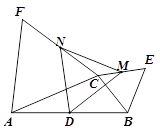
求证：△DMN是等边三角形；
连接EF，Q是EF中点，CP⊥EF于点P. 求证：DP＝DQ.
同学们，如果你觉得解决本题有困难，可以阅读下面两位同学的解题思路作为参考：
小聪同学发现此题条件中有较多的中点，因此考虑构造三角形的中位线，添加出了一些辅助线；小慧同学想到要证明线段相等，可通过证明三角形全等，如何构造出相应的三角形呢？她考虑将△NCM绕顶点旋转到要证的对应线段的位置，由此猜想到了所需构造的三角形的位置.
是三个连续的正整数
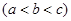，以b为边长作正方形，分别以c，
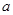为长和宽作长方形，哪个图形的面积大？为什么？
推理填空，如图
1、如图，已知∠A=∠F，∠C=∠D，试说明BD∥CE.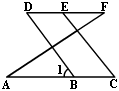
解：∵∠A=∠F(已知)
∴AC∥DF()
∴∠D=∠( )
又∵∠C=∠D(已知)
∴∠1=∠C(等量代换)
∴BD∥CE( )
作图题（尺规作图，不写作法，但保留作图痕迹）
如图，已知，∠α 、∠β。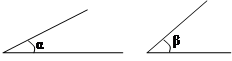
求作∠AOB,使∠AOB =2∠α+∠β，
先化简，再求值：
，其中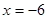
正方形ABCD中，E点为BC中点，连接AE，过B点作BF⊥AE，交CD于F点，交AE于G点，连接GD，过A点作AH⊥GD交GD于H点．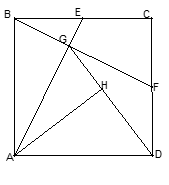
(1) 求证：△ABE≌△BCF；
(2) 若正方形边长为4，AH =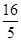
，求△AGD的面积．