在平面直角坐标系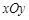
中，抛物线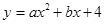
经过A（－3,0）、B（4,0）两点，且与y轴交于点C，点D在x轴的负半轴上，且BD＝BC，有一动点P从点A出发，沿线段AB以每秒1个单位长度的速度向点B移动，同时另一个动点Q从点C出发，沿线段CA以某一速度向点A移动.
求该抛物线的解析式；
若经过t秒的移动，线段PQ被CD垂直平分，求此时t的值；
该抛物线的对称轴上是否存在一点M，使MQ＋MA的值最小？若存在，求出点M的坐标；若不存在，请说明理由.
作图题：（不写作法，但必须保留作图痕迹）
如图：某地有两所大学和两条相交叉的公路，（点M，N表示大学，AO，BO表示公路）.现计划修建一座物资仓库，希望仓库到两所大学的距离相等，到两条公路的距离也相等。你能确定仓库P应该建在什么位置吗？在所给的图形中画出你的设计方案。
如图，已知AB=AC，D、E分别为AB、AC上两点，∠B=∠C，求证：BD=CE。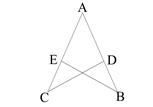
如图：AE=DE，BE=CE，AC和BD相交于点E，求证：AB=DC
计算： 
如图，将一张正方形纸片，剪成四个大小形状一样的小正方形，然后将其中的一个小正方形再按同样的方法剪成四个小正方形，再将其中的一个小正方形剪成四个小正方形，如此循环进行下去。
（1）填表：
| 剪的次数 （剪两刀记一次） |
1 |
2 |
3 |
4 |
5 |
6 |
| 正方形个数 |
4 |
7 |
（2）如果剪n次，共剪出多少个正方形？
（3）如果剪了100次，共剪出多少个正方形？