阅读并回答问题:
小亮是一位刻苦学习、勤于思考、勇于创新的同学.一天他在解方程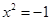 时,突发
时,突发
奇想: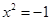 在实数范围内无解,如果存在一个数i,使
在实数范围内无解,如果存在一个数i,使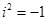 ,那么当
,那么当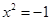 时,有
时,有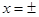 i,从而
i,从而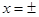 i是方程
i是方程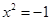 的两个根.
的两个根.
据此可知: i可以运算,例如:i3=i2·i=-1×i=-i,则i4= ,
i2011=______________,i2012=__________________;方程
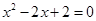 的两根为 (根用i表示).
的两根为 (根用i表示).
一个可自由转动的圆盘,被分成12块相等的扇形,其中有3 块染上了红色,4块染上了绿色,其余都染上了黄色,转盘停止时, 指针落在下列颜色区域的概率各是多少?毛
(1)红色,(2)黄色,(3)不是绿色,(4)不是黄色
某沿海城市将进行旧城改造,该市地区面积约占40%,其余为郊区, 计划将城区面积的40%建成“公寓式”住宅,面积占城区30% 的工厂迁至北部郊区的荒废地带,其余均为商业区,而郊区的北部已有工厂占郊区面积的20%,南部沿海一带将被开发为别墅区占20%,原占地40%农田不变.当电脑把该市新城郊规划图显示在屏幕上时,任意点击一下鼠标,则被点击点是下列位置的概率是多少?
(1)别墅区,(2)居住区,(3)商业区,(4)工业区
学校教学楼内一层楼有10个教室,小丁、小新、小丽分别在其中的一个教室内,王老师有事想找他们,请你算出王老师任意走进一个教室找到他们中一个的概率.
小阳和小鸣掷一对骰子,如果小阳掷出的骰子点数之和为6,则加1分,否则不得分;如果小鸣掷出的点数之和为7,则加1分;否则不得分.他们各掷20次,记录每次得分,20次累计分高的为胜,这个游戏对小阳和小鸣双方公平吗?说明你的理由,和同桌交流.
小璐和小丽都想去参加一项重要的比赛,但只有一个名额.于是他们决定抓阄,一张写着yes,一张写着no,抓住yes的就去,抓住no的就不去.这对双方公平吗?