已知,△ABC为等边三角形,点D为直线BC上一动点(点D不与B、C重合).以AD为边作菱形ADEF,使∠DAF=60°,连接CF.如图1,当点D在边BC上时,
①求证:∠ADB=∠AFC;②请直接判断结论∠AFC=∠ACB+∠DAC是否成立;如图2,当点D在边BC的延长线上时,其他条件不变,结论∠AFC=∠ACB+∠DAC是否成立?请写出∠AFC、∠ACB、∠DAC之间存在的数量关系,并写出证明过程;
如图3,当点D在边CB的延长线上时,且点A、F分别在直线BC的异侧,其他条件不变,请补全图形,并直接写出∠AFC、∠ACB、∠DAC之间存在的等量关系.

如图,抛物线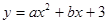 与x轴交于点A(1,0)和B(3,0).
与x轴交于点A(1,0)和B(3,0).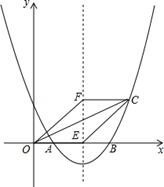
(1)求抛物线的解析式;
(2)若抛物线的对称轴交x轴于点E,点F是位于x轴上方对称轴上一点,FC∥x轴,与对称轴右侧的抛物线交于点C,且四边形OECF是平行四边形,求点C的坐标;
(3)在(2)的条件下,抛物线的对称轴上是否存在点P,使△OCP是等腰三角形?若存在,请直接写出点P的坐标;若不存在,请说明理由.
如图,二次函数y=ax2+bx+c的图象交x轴于A(﹣1,0),B(2,0),交y轴于C(0,﹣2),过A,C画直线.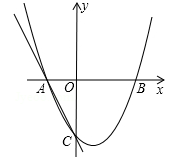
(1)求二次函数的解析式;
(2)点P在x轴正半轴上,且PA=PC,求OP的长;
(3)若M为线段OB上一个动点,过点M作MN平行于y轴交抛物线于点N,当点M运动到何处时,四边形ACNB的面积最大?求出此时点M的坐标及四边形ACNB面积的最大值.
如图,对称轴为x=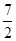 的抛物线经过点A(6,0)和B(0,4).
的抛物线经过点A(6,0)和B(0,4).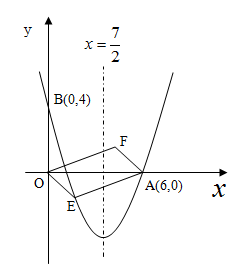
(1)求抛物线解析式;
(2)设点E(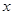 ,
,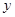 )是抛物线上一动点,且位于第四象限,四边形OEAF是以OA为对角线的平行四边形.求平行四边形OEAF的面积S与
)是抛物线上一动点,且位于第四象限,四边形OEAF是以OA为对角线的平行四边形.求平行四边形OEAF的面积S与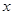 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量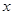 的取值范围;
的取值范围;
①当平行四边形OEAF的面积为24时,请判断平行四边形OEAF是否为菱形?
②是否存在点E,使平行四边形OEAF为正方形?若存在,求出点E的坐标;若不存在,请说明理由.
如图,抛物线y=ax2+bx+c经过点A(﹣3,0),B(1,0),C(0,﹣3).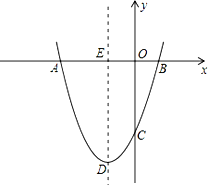
(1)求抛物线的解析式;
(2)若点P为第三象限内抛物线上的一点,设△PAC的面积为S,求S的最大值并求出此时点P的坐标;
(3)设抛物线的顶点为D,DE⊥x轴于点E,在y轴上是否存在点M,使得△ADM是直角三角形?若存在,请直接写出点M的坐标;若不存在,请说明理由.
如图,二次函数的图象与x轴交与A(4,0),并且OA=OC=4OB,点P为过A、B、C三点的抛物线上一动点.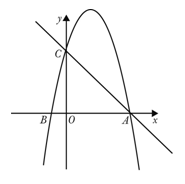
(1)求点B、点C的坐标并求此抛物线的解析式;
(2)是否存在点P,使得△ACP是以点C为直角顶点的直角三角形?若存在,求出点P的坐标;若不存在,说明理由;
(3)过动点P作PE垂直于y轴于点E,交直线AC于点D,过点D作x轴的垂线,垂足为F,连接EF,当线段EF的长度最短时,求出点P的坐标.