如图,在矩形ABCD中,AB=12cm,BC=8cm,点E,F,G分别从点A,B,C三点同时出发,沿矩形的边按逆时针方向移动,点E,G的速度均为2cm/s,点F的速度为4cm/s,当点F追上点G(即点F与点G重合)时,三个点随之停止移动.设移动开始后第t秒时,△EFG的面积为S(cm2).当t=1秒时,S的值是多少?
写出S和t之间的函数解析式,并指出自变量t的取值范围.
若点F在矩形的边BC上移动,当t为何值时,以点E,B,F为顶点的三角形与以F,C,G为顶点的三角形相似?请说明理由.

将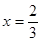 代入反比例函数
代入反比例函数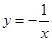 中,所得函数值记为
中,所得函数值记为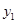 ,又将
,又将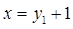 代入反比例函数的关系式中,所得函数值记为
代入反比例函数的关系式中,所得函数值记为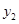 ,再将
,再将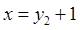 代入反比例函数中,所得函数值记为
代入反比例函数中,所得函数值记为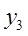 ,……,如此继续下去,则
,……,如此继续下去,则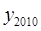 =_____________.
=_____________.
如图,E、F是平行四边形ABCD对角线BD上的两点,请你添上一个适当的条件:
,使四边形AECF为平行四边形.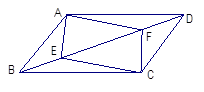
(1)如图①,在正方形ABCD中,△AEF的顶点E,F分别在BC,CD边上,高AG与正方形的边长相等,求∠EAF的度数.
(2)如图②,在Rt△ABD中,∠BAD=90°,AB=AD,点M,N是BD边上的任意两点,且∠MAN=45°,将△ABM绕点A逆时针旋转90°至△ADH位置,连接NH,试判断MN,ND,DH之间的数量关系,并说明理由.
(3)在图①中,连接BD分别交AE,AF于点M,N,若EG=4,GF=6,BM=3,求AG,MN的长.
已知关于x的方程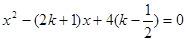
(1)求证:不论k取什么实数值,这个方程总有实数根;
(2)若等腰三角形ABC的一边长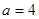 ,另两边的长b,c恰好是这个方程的两根,求△ABC的周长。
,另两边的长b,c恰好是这个方程的两根,求△ABC的周长。
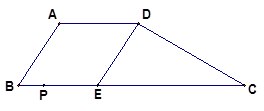
如图,在梯形ABCD中,AD∥BC,E是BC上的一点,且CE=8,BC=12,CD=4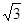 ,∠C=30°,∠B=60°。点P是线段BC边上一动点(包括B、C两点),设PB的长是x。
,∠C=30°,∠B=60°。点P是线段BC边上一动点(包括B、C两点),设PB的长是x。
(1)当x为何值时,以点P、A、D、E为顶点的四边形为直角梯形。
(2)当x为何值时,以点P、A、D、E为顶点的四边形为平行四边形。
(3)P在BC 上运动时,以点P、A、D、E为顶点的四边形能否为菱形。