如图是某货站传送货物的平面示意图. 为了提高传送过程的安全性,工人师傅欲减小传送带与地面的夹角,使其由45°改为30°. 已知原传送带AB长为4米.求新传送带AC的长度;
如果需要在货物着地点C的左侧留出2米的通道,试判断距离B点4米的货物MNQP是否需要挪走,并说明理由.(说明:⑴⑵的计算结果精确到0.1米,参考数据:
 ≈1.41,
≈1.41, ≈1.73,
≈1.73, ≈2.24,
≈2.24, ≈2.45)
≈2.45)
解方程(2×5)
(1)
(2)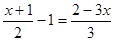
计算(4×4)
(1)
(2)
(3)
(4)
【问题提出】学习了三角形全等的判定方法(即“SAS”、“ASA”、“AAS”、“SSS”)和直角三角形全等的判定方法(即“HL”)后,我们继续对“两个三角形满足两边和其中一边的对角对应相等”的情形进行研究.
【初步思考】我们不妨将问题用符号语言表示为:在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E,然后,对∠B进行分类,可分为“∠B是直角、钝角、锐角”三种情况进行探究.
【深入探究】
第一种情况:当∠B是直角时,△ABC≌△DEF.
(1)如图①,在△ABC和△DEF,AC=DF,BC=EF,∠B=∠E=90°,根据,可以知道Rt△ABC≌Rt△DEF.
第二种情况:当∠B是钝角时,△ABC≌△DEF.
(2)如图②,在△ABC和△DEF,AC=DF,BC=EF,∠B=∠E,且∠B.∠E都是钝角,求证:△ABC≌△DEF.
第三种情况:当∠B是锐角时,△ABC和△DEF不一定全等.
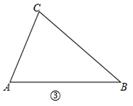
(3)在△ABC和△DEF,AC=DF,BC=EF,∠B=∠E,且∠B.∠E都是锐角,请你用尺规在图③中作出△DEF,使△DEF和△ABC不全等.(不写作法,保留作图痕迹)
(4)∠B还要满足什么条件,就可以使△ABC≌△DEF?请直接写出结论:在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E,且∠B.∠E都是锐角,若,则△ABC≌△DEF.
在Rt△ABC中,∠CAB=90°,AB=AC.
(1)如图①,过点A在△ABC外作直线MN,BM⊥MN于M,CN⊥MN于N.
①判断线段MN、BM、CN之间有何数量关系,并证明;
②若AM= ,BM=
,BM= ,AB=
,AB= ,试利用图①验证勾股定理
,试利用图①验证勾股定理 =
= ;
;
(2)如图②,过点A在△ABC内作直线MN,BM⊥MN于M,CN⊥MN于N,判断线段MN、BM、CN之间有何数量关系?(直接写出答案)
如图①,在△ABC中,AB=AC,点D是BC的中点,点E在AD上.
(1)求证:BE=CE;
(2)若BE的延长线交AC于点F,且BF⊥AC,垂足为F,如图②,∠BAC=45°,原题设其它条件不变.求证:△AEF≌△BCF.