(本小題满分12分)如图,直角梯形ABCD中,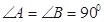 ,AD =" AB" = 2, BC = 3,E,F分别是AD,BC上的两点,且AE=BF=1,G为AB中点,将四边形ABCD沿EF折起到(如图2)所示的位置,使得EG丄GC,连接 AD、BC、AC得(图2)所示六面体.
,AD =" AB" = 2, BC = 3,E,F分别是AD,BC上的两点,且AE=BF=1,G为AB中点,将四边形ABCD沿EF折起到(如图2)所示的位置,使得EG丄GC,连接 AD、BC、AC得(图2)所示六面体.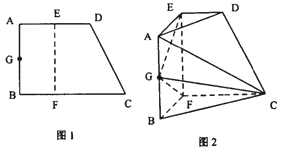
(1)求证:EG丄平面CFG;
(2)求二面角A —CD-E的余弦值.
(本小题满分12分)我市某中学一研究性学习小组,在某一高速公路服务区,从小型汽车中按进服务区的先后,每间隔5辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调查,将他们在某段高速公路的车速(km/h)分成六段: 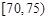 ,
,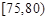 ,
,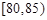 ,
, ,
, ,
,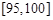 ,统计后得到如图的频率分布直方图.
,统计后得到如图的频率分布直方图.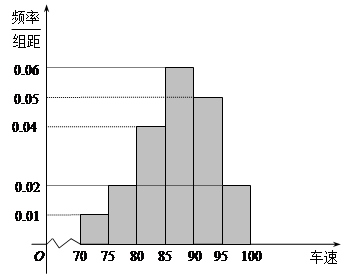
(1)此研究性学习小组在采样中,用到的是什么抽样方法?并求这40辆小型汽车车速的众数和中位数的估计值.
(2)从车速在 的车辆中任意抽取3辆车,求车速在
的车辆中任意抽取3辆车,求车速在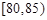 ,
, 内都有车辆的概率.
内都有车辆的概率.
(3)若从车速在 的车辆中任意抽取3辆,求车速在
的车辆中任意抽取3辆,求车速在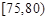 的车辆数的数学期望.
的车辆数的数学期望.
(本小题满分12分)在如图所示的平面直角坐标系中,已知点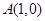 和点
和点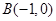 ,
, ,且
,且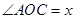 ,其中
,其中 为坐标原点.
为坐标原点.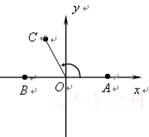
(1)若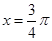 ,设点
,设点 为线段
为线段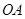 上的动点,求
上的动点,求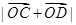 的最小值;
的最小值;
(2)若 ,向量
,向量 ,
,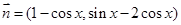 ,求
,求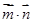 的最小值及对应的
的最小值及对应的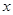 值.
值.
《选修4-5:不等式选讲》已知函数 .
.
(1)证明: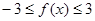 ;
;
(2)求不等式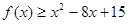 的解集.
的解集.
《选修4-4:坐标系与参数方程》已知直线L的参数方程: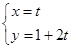 (t为参数)和圆C的极坐标方程:
(t为参数)和圆C的极坐标方程: 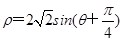 (θ为参数).
(θ为参数).
(1)求圆C的直角坐标方程.
(2)判断直线L和圆C的位置关系.