推理证明:如图,已知△ABC中,AB=BC,以AB为直径的⊙O交AC于点D过D作DE⊥BC,垂足为E,连结OE,CD=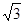 ,∠ACB=30°.
,∠ACB=30°.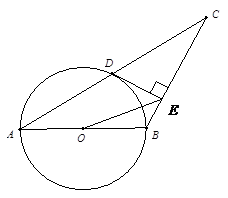
(1)求证:DE是⊙O的切线;
(2)分别求AB,OE的长;
(3)填空:如果以点E为圆心,r为半径的圆上总存在不同的两点到点O的距离为1,则r的取值范围为 .
如图,已知扇形AOB中,∠AOB=120°,弦AB=2 ,点M是弧AB上任意一点(与端点A、B不重合),ME⊥AB于点E,以点M为圆心、ME长为半径作⊙M, 分别过点A、B作⊙M的切线,两切线相交于点C.
,点M是弧AB上任意一点(与端点A、B不重合),ME⊥AB于点E,以点M为圆心、ME长为半径作⊙M, 分别过点A、B作⊙M的切线,两切线相交于点C.
(1)求弧AB的长;
(2)试判断∠ACB的大小是否随点M的运动而改变,若不变,请求出∠ACB的大小;若改变,请说明理由.
快、慢两车分别从相距480km的甲、乙两地同时出发,匀速行驶,先相向而行,途中慢车因故停留了1小时,然后继续以原速驶向甲地,到达甲地后即停止行驶;快车到达乙地后,立即按原路原速返回甲地(调头时间忽略不计).如图是快、慢两车距乙地路程y(km)与所用时间x(h)之间的函数图像,结合图像解答下列问题: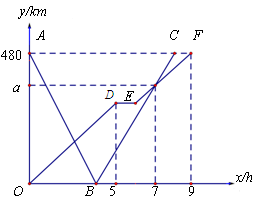
(1)求慢车的行驶速度和a的值.
(2)快车与慢车第一次相遇时,距离甲地的路程是多少千米?
(3)两车出发后几小时相距的路程为200千米?
在一个盒子中装有红球、绿球、白球各1个,这3个球除颜色外其余都相同,小明先从盒子中摸出2个球后放回,小李再从盒子中摸出2个球.请用列表或画树状图法求他们摸到的4个球恰好包含所有颜色的概率.
为了解某校九年级学生体育模考情况,现从中随机抽取部分学生的体育模考成绩统计如下,其中扇形统计图中的圆心角α为36°.
九年级学生体育模考成绩统计表
| 体育成绩 |
人数(人) |
百分比(%) |
| 26 |
||
| 27 |
m |
|
| 28 |
8 |
16 |
| 29 |
24 |
|
| 30 |
15 |

根据上面提供的信息,回答下列问题:
(1)m=;抽取的部分学生体育模考成绩的中位数为;
(2)已知该校九年级共有500名学生,如果体育模考成绩达29分(含29分)为优秀,请估计该校九年级学生体育模考成绩达到优秀的总人数.
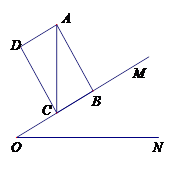
如图,已知∠MON=25°,矩形ABCD的边BC在OM上,对角线AC⊥ON.当AC=5时,求AD的长.(参考数据:sin25°=0.42;cos25°=0.91;tan25°=0.47,结果精确到0.1)