为增强学生的身体素质,教育行政部门规定学生每天参加户外活动的平均时间不少于1小时.为了解学生参加户外活动的情况,对部分学生参加户外活动的时间进行抽样调查,并将调查结果绘制作成如下两幅不完整的统计图,请你根据图中提供的信息解答下列问题:
⑴在这次调查中共调查了多少名学生?并补充频数分布直方图;
⑵求表示户外活动时间1小时的扇形圆心角的度数。
(3)本次调查中学生参加户外活动的平均时间是否符合要求?并写出户外活动时间的众数和中位数是多少?
甲骑自行车、乙骑摩托车沿相同路线由A地到B地,行驶过程中路程与时间的函数关系的图象如图. 根据图象解决下列问题:
(1) 谁先出发?先出发多少时间?谁先到达终点?先到多少时间?(2) 分别求出甲、乙两人的行驶速度;(3) 在什么时间段内,两人均行驶在途中(不包括起点和终点)?在这一时间段内,请你根据下列情形,分别列出关于行驶时间x的方程或不等式(不化简,也不求解):① 甲在乙的前面;② 甲与乙相遇;③ 甲在乙后面.
雨伞的中截面如图所示,伞骨AB=AC,支撑杆OE=OF,AE= AB,AF=
AB,AF= AC,当O沿AD滑动时,雨伞开闭,问雨伞开闭过程中,∠BAD与∠CAD有何关系?说明理由.
AC,当O沿AD滑动时,雨伞开闭,问雨伞开闭过程中,∠BAD与∠CAD有何关系?说明理由.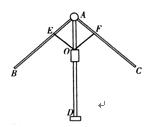
已知一个正比例函数和一个一次函数,它们的图象都经过点P(-3,3),且一次函数的图象与y轴相交于Q(0,-2),求这两个函数的解析式.
D是AB上一点,DF交AC于点E,DE=EF,AE=CE,求证:AB∥CF。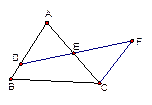
如图,在△ABC中,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别是E,F,BE=CF.求证:AD是△ABC的角平分线。