△ABC在平面直角坐标系中的位置如图所示: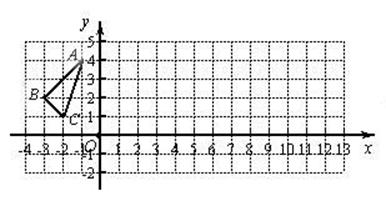
①作出△ABC关于y轴对称的△A1B1C1,并写出△A1B1C1各顶点的坐标;
②将△ABC向右平移8个单位,作出平移后的△A2B2C2,并写出△A2B2C2各顶点的坐标;
③观察△A1B1C1与△A2B2C2它们是否关于某直成对称?若是,请在图上画出这条对称轴.
小明同学用纸板制作了一个圆锥形漏斗模型,如图所示,它的底面半径OB=3cm,高OC=4cm,求这个圆锥形漏斗的侧面积.
解方程:
如图,一次函数的图象与x轴、y轴分别交于A、B两点,与反比例函数的图象交于C、D两点,如果A点的坐标为(2,0),点C、D分别在第一、三象限,且OA=OB=AC=BD,试求一次函数和反比例函数的解析式.
反比例函数y=- 与直线y=-x+2的图象交于A、B两点,点A、B分别在第四、二象限,求:
与直线y=-x+2的图象交于A、B两点,点A、B分别在第四、二象限,求:
(1)A、B两点的坐标;
(2)△ABO的面积.
如图,第一象限的角平分线OM与反比例函数的图象相交于点A,已知OA=2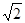 .
.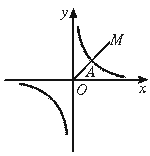
(1)求点A的坐标;
(2)求此反比例函数的解析式.