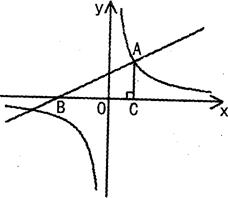
如图，一次函数y=" kx" +2的图象与x轴交于点B，与反比例函数y=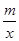
的图象的一个交点为A(2，3)．分别求出反比例函数和一次函数的解析式；
过点A作AClx轴，垂足为C，若点P在反比例函数图象上，且APBC的面积等于18，求P点的坐标．
列方程解应用题：国家规定个人发表文章、出版著作所获稿费应纳税，其计算方法是：① 稿费不高于800元免税；②稿费高于800元但不高于4000元，应缴纳超过800元的那一部分的14%；③稿费高于4000元应缴纳全部稿费的11%的税.
今知李教授出版一部著作获得一笔稿费，他缴了550元的税，那么李教授的这笔稿费是多少元？
列方程解应用题：某种型号的出租车起价是10元（即行驶路程在4km以内或4km都需付10元车费），超过4km后，每增加1km加价1.2元（不足1km部分按1km计）.现在某人乘这种出租汽车从甲地到乙地，支付车费19.6元，从甲地到乙地的路程大约是多少千米？
列方程解应用题：某学校在援助边远山区学校活动中，原计划赠书3000册，由于学生的积极响应，实际赠书3780册，其中初中部比原计划多赠了20%，高中部比原计划多赠了30%，该校初、高中部原计划各赠书多少册？
列方程解应用题：出租车10元起价，行驶4km以后，每增加1km加价1.2元（不足1km部分按1km计）.小明要乘出租车去10km外的叔叔家，出门时只拿了16元钱，小明能否乘出租车直接到叔叔家？（不计等候时间）
列方程解应用题：甲、乙两班计划共同植树360棵，结果由于同学们的积极努力，甲班超额完成计划的12%，乙班超额完成计划的10%，因此，两班实际植树400棵.甲、乙两班原计划各植多少棵树？