如图,在平面直角坐标系中,等腰直角三角形OMN的斜边ON在x轴上,顶点M的坐标为(3,3),MH为斜边上的高.过N点垂直于x轴的直线与抛物线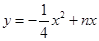 y=" -" 4x点D.直线OD的解析式为
y=" -" 4x点D.直线OD的解析式为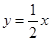 ,点P(x,o)是x轴上一动点,过点P作y轴的平行线,交射线OM与点E.
,点P(x,o)是x轴上一动点,过点P作y轴的平行线,交射线OM与点E.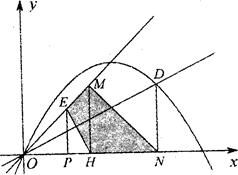
直接写出点D的坐标及n的值
判断抛物线的顶点是否在直线OM上?并说明理由
设以M、E、H、N为顶点的四边形的面积为S.当x≠3[时,求S与x的函数关系式.
(·湖北黄冈,24题,分)(14 分)如图,在矩形OABC 中,OA=5,AB=4,点D 为边AB 上一点,将△BCD 沿直线CD 折叠,使点B 恰好落在OA边上的点E 处,分别以OC,OA 所在的直线为x 轴,y 轴建立平面直角坐标系.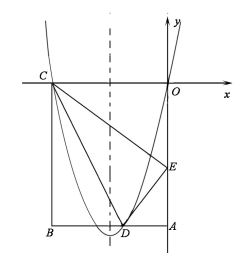
(1)求OE 的长;
(2)求经过O,D,C 三点的抛物线的解析式;
(3)一动点P 从点C 出发,沿CB 以每秒2 个单位长的速度向点B 运动,同时动点Q 从E 点出发,沿EC 以每秒1 个单位长的速度向点C 运动,当点P 到达点B 时,两点同时停止运动.设运动时间为t 秒,当t为何值时,DP=DQ;
(4) 若点N 在(2)中的抛物线的对称轴上,点M 在抛物线上,是否存在这样的点M与点N,使得以M,N,C,E 为顶点的四边形是平行四边形?若存在,请求出M 点的坐标;若不存在,请说明理由.
(·湖北黄冈,22题,分)(8 分)如图,反比例函数 的图象经过点A(
的图象经过点A( ,4),直线
,4),直线 (
( )与双曲线
)与双曲线 在第二、四象限分别相交于P,Q 两点,与x轴、y 轴分别相交于C,D 两点.
在第二、四象限分别相交于P,Q 两点,与x轴、y 轴分别相交于C,D 两点.
(1)求k 的值;
(2)当 时,求△OCD 的面积;
时,求△OCD 的面积;
(3)连接OQ,是否存在实数b,使得 ? 若存在,请求出b 的值;若不存在,请说明理由.
? 若存在,请求出b 的值;若不存在,请说明理由.
(·湖北衡阳,27题,分)(本小题满分10分)如图,顶点M在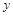 轴上的抛物线与直线
轴上的抛物线与直线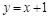 相交于A、B两点,且点A在
相交于A、B两点,且点A在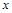 轴上,点B的横坐标为2,连结AM、BM.
轴上,点B的横坐标为2,连结AM、BM.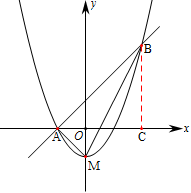
(1)求抛物线的函数关系式;
(2)判断△ABM的形状,并说明理由;
(3)把抛物线与直线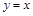 的交点称为抛物线的不动点.若将(1)中抛物线平移,使其顶点为(
的交点称为抛物线的不动点.若将(1)中抛物线平移,使其顶点为(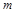 ,
,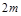 ),当
),当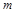 满足什么条件时,平移后的抛物线总有不动点?
满足什么条件时,平移后的抛物线总有不动点?
(·湖南株洲)已知AB是圆O的切线,切点为B,直线AO交圆O于C、D两点,CD=2,∠DAB=30°,动点P在直线AB上运动,PC交圆O于另一点Q,
(1)当点P,运动到Q、C两点重合时(如图1),求AP的长。
(2)点运动过程中,有几个位置(几种情况)使△CQD的面积为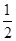 ?( 直接写出答案)
?( 直接写出答案)
(3)当使△CQD的面积为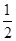 ,且Q位于以CD为直径的的上半圆上,CQ>QD时(如图2),求AP的长。
,且Q位于以CD为直径的的上半圆上,CQ>QD时(如图2),求AP的长。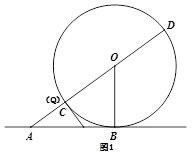
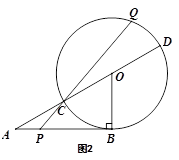
(·湖南长沙)如图,在直角坐标系中,⊙M经过原点O(0,0),点A(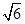 ,0)与点B(0,-
,0)与点B(0,-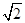 ),点D在劣弧OA上,连接BD交x轴于点C,且∠COD=∠CBO。
),点D在劣弧OA上,连接BD交x轴于点C,且∠COD=∠CBO。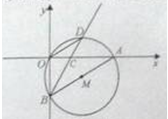
(1)求⊙M的半径;
(2)求证:BD平分∠ABO;
(3)在线段BD的延长线上找一点E,使得直线AE恰为⊙M的切线,求此时点E的坐标。