(·湖北衡阳,27题,分)(本小题满分10分)如图,顶点M在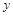 轴上的抛物线与直线
轴上的抛物线与直线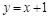 相交于A、B两点,且点A在
相交于A、B两点,且点A在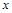 轴上,点B的横坐标为2,连结AM、BM.
轴上,点B的横坐标为2,连结AM、BM.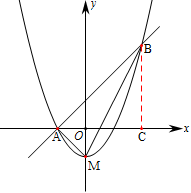
(1)求抛物线的函数关系式;
(2)判断△ABM的形状,并说明理由;
(3)把抛物线与直线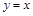 的交点称为抛物线的不动点.若将(1)中抛物线平移,使其顶点为(
的交点称为抛物线的不动点.若将(1)中抛物线平移,使其顶点为(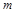 ,
,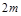 ),当
),当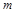 满足什么条件时,平移后的抛物线总有不动点?
满足什么条件时,平移后的抛物线总有不动点?
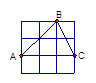
一个包装盒的设计方法如图所示,ABCD是边长为60cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得 四个点重合于图中的点P,正好形成一个正四棱柱形状的包装盒,E、F在AB上是被切去的等腰直角三角形斜边的两个端点,设AE =" FB" = xcm。若广告商要求包装盒侧面积S(cm
四个点重合于图中的点P,正好形成一个正四棱柱形状的包装盒,E、F在AB上是被切去的等腰直角三角形斜边的两个端点,设AE =" FB" = xcm。若广告商要求包装盒侧面积S(cm )大,试问x应取的值为cm.
)大,试问x应取的值为cm.

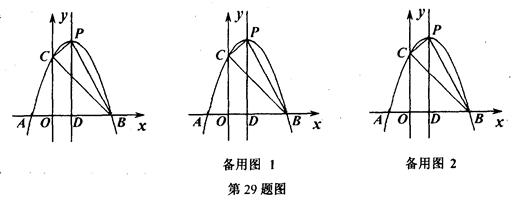
如图,在正方形网格中,sin =.
=.
如图,抛物线y=ax2+bx+c的顶点为P,对称轴直线x=1与x轴交于点D,抛物线与x轴交于A、B两点,与y轴交于点C,其中A(-1,0)、C(0,3).求此抛物线的解析式
点E在线段BC上,若△DEB为等腰三角形,求点E的坐标
点F、Q都在该抛物线上,若点C与点F关于直线x=1成轴对称,连结BF、BQ,如果∠FBQ=45°,求点Q的坐标;
将△BOC绕着它的顶点B顺时针在第一象限内旋转,旋转后的图形为△BO'C',BO'与BP重合时,则△BO'C'不在BP上的顶点C'的坐标为▲(直接写出答案).
如图(1),(2)所示,矩形ABCD的边长AB=6,BC=4,点F在DC
上,DF=2.动点M、N分别从点D、B同时出发,沿射线DA、线段BA向点A的方向运动(点M可运动到DA的延长线上),当动点N运动到点A时,M、N两点同时停止运动.连接FM、MN、FN,当F、N、M不在同一直线时,可得△FMN,过△FMN三边的中点作△PQW.设动点M、N的速度都是1个单位/秒,M、N运动的时间为x秒.试解答下列问题:DM=___▲____, AN=___▲____(用含x的代数式表示)
说明△FMN
 ∽ △QWP;
∽ △QWP;试问
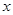 为何值时,△PQW为直角三角形?
为何值时,△PQW为直角三角形? 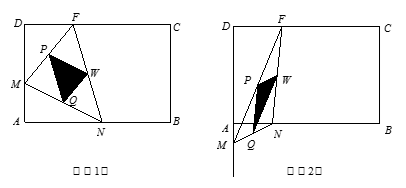
问当
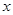 为____▲_____时,线段MN最短?
为____▲_____时,线段MN最短?
已知:如图,DABC内接于⊙O,AB为直径,∠CBA的平分线交AC于点F,交⊙O于点D,DE⊥AB于点E,且交AC于点P,连结AD. 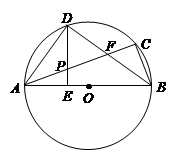
求证:∠DAC =∠DBA;
求证:
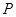 是线段AF的中点
是线段AF的中点若⊙O 的半径为5,AF =
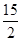 ,求tan∠ABF的值.
,求tan∠ABF的值.