一个包装盒的设计方法如图所示,ABCD是边长为60cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得 四个点重合于图中的点P,正好形成一个正四棱柱形状的包装盒,E、F在AB上是被切去的等腰直角三角形斜边的两个端点,设AE =" FB" = xcm。若广告商要求包装盒侧面积S(cm
四个点重合于图中的点P,正好形成一个正四棱柱形状的包装盒,E、F在AB上是被切去的等腰直角三角形斜边的两个端点,设AE =" FB" = xcm。若广告商要求包装盒侧面积S(cm )大,试问x应取的值为 cm.
)大,试问x应取的值为 cm.

解方程:(1) 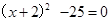 ;(2)x2+4x-2=0(用配方法);(3)
;(2)x2+4x-2=0(用配方法);(3)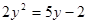 .
.
课本中把长与宽之比为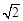 的矩形纸片称为标准纸.请解决下列问题:
的矩形纸片称为标准纸.请解决下列问题:
(1)将一张标准纸ABCD(AB<BC)对开,如图1所示,所得的矩形纸片ABEF是标准纸.请给予证明;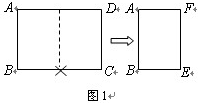
(2)在一次综合实践课上,小明尝试着将矩形纸片ABCD(AB<BC)进行如下操作:
第一步:沿过A点的直线折叠,使B点落在AD边上点F处,折痕为AE(如图2甲);
第二步:沿过D点的直线折叠,使C点落在AD边上点N处,折痕为DG(如图2乙) .此时E点恰好落在AE边上的点M处;
第三步:沿直线DM折叠(如图2丙),此时点G恰好与N点重合.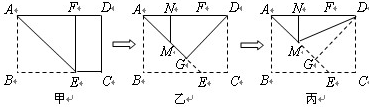
请你研究,矩形纸片ABCD是否是一张标准纸?请说明理由.
(3)不难发现,将一张标准纸如图3一次又一次对开后,所得的矩形纸片都是标准纸.现有一张标准纸ABCD,AB=1,BC=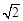 ,问第5次对开后所得标准纸的周长是多少?探索并直接写出第2002次对开后所得标准纸的周长.
,问第5次对开后所得标准纸的周长是多少?探索并直接写出第2002次对开后所得标准纸的周长.
某汽车销售公司6月份销售某厂家的汽车,在一定范围内,每部汽车的进价与销售有如下关系,若当月仅售出一部汽车,则该部汽车的进价为27万元,每多售一部,所有出售的汽车的进价均降低0.1万元/部。月底厂家根据销售量一次性返利给销售公司,销售量在10部以内,含10部,每部返利0.5万元,销售量在10部以上,每部返利1.3万元。
①若该公司当月卖出4部汽车,则每部进价为万元;
②如果汽车的销售价位28万元/部,该公司计划当月盈利24万元,那么要卖出多少部汽车?(盈利=利润+返利).
如图1,△ABC是等腰直角三角形,∠BAC=90°,AB=AC,四边形ADEF是正方形,D、F分别在AB、AC边上,此时BD=CF,BD⊥CF成立.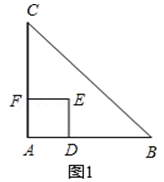
(1)当正方形ADEF绕点A逆时针旋转θ(0°<θ<90°)时,如图2,BD=CF成立吗?若成立,请证明;若不成立,请说明理由.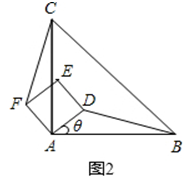
(2)当正方形ADEF绕点A逆时针旋转45°时,如图3,延长BD交CF于点G.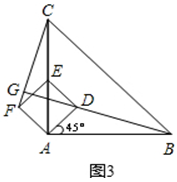
①求证:BD⊥CF;
②当AB=4,AD= 时,求线段FG的长.
时,求线段FG的长.
已知:关于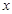 的一元二次方程
的一元二次方程 .
.
(1)求实数k的取值范围;
(2)设上述方程的两个实数根分别为x1、x2,求:当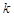 取哪些整数时,x1、x2均为整数;
取哪些整数时,x1、x2均为整数;
(3)设上述方程的两个实数根分别为x1、x2,若 ,求k的值.
,求k的值.