课本中把长与宽之比为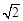
的矩形纸片称为标准纸．请解决下列问题：
（1）将一张标准纸ABCD(AB＜BC)对开，如图1所示，所得的矩形纸片ABEF是标准纸．请给予证明；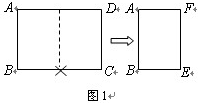
（2）在一次综合实践课上，小明尝试着将矩形纸片ABCD(AB＜BC)进行如下操作：
第一步：沿过A点的直线折叠，使B点落在AD边上点F处，折痕为AE(如图2甲)；
第二步：沿过D点的直线折叠，使C点落在AD边上点N处，折痕为DG(如图2乙) ．此时E点恰好落在AE边上的点M处；
第三步：沿直线DM折叠（如图2丙），此时点G恰好与N点重合．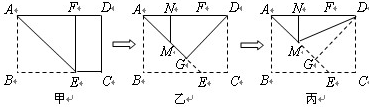
请你研究，矩形纸片ABCD是否是一张标准纸？请说明理由．
（3）不难发现，将一张标准纸如图3一次又一次对开后，所得的矩形纸片都是标准纸．现有一张标准纸ABCD，AB＝1，BC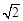＝，问第5次对开后所得标准纸的周长是多少？探索并直接写出第2002次对开后所得标准纸的周长．
某班同学参加公民道德知识竞赛，将竞赛所得的成绩（得分取整数）进行整理后分成五组，并绘制成条形统计图，根据图中提供的信息，回答下列问题：
（1）人数最多的学生在分数段．
（2）69.5～79.5这一分数段的频数是，频率是．（精确到0.01）
（3）如果60分以上为及格分（含60分），请估计本班的及格率为．（精确到0.001）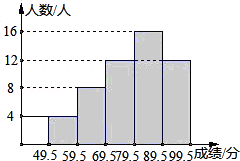
在一个样本中，已知一组数据分别落在五个小组内，第一、二、三、五组数据的个数分别是2，8，15，5，且第五组的频率为0.1，则这个样本中数据的总数是个，第四组的频数和频率分别是．
思考题：在对某地区的一次人口抽样统计分析中，各年龄段（年龄为整数）的人数如下表所示：
| 年龄段 |
0～9 |
10～19 |
20～29 |
30～39 |
40～49 |
50～59 |
60～69 |
70～79 |
80～89 |
| 人数 |
9 |
11 |
17 |
18 |
17 |
12 |
8 |
6 |
2 |
根据此表回答下列问题：
（1）样本中年龄在60岁以上（含60岁）的频率是；
（2）如果该地区现有人口80000人，为关注人口老龄化问题，请估算该地区60岁以上（含60岁）的人口数．
学期结束前，学校想调查学生对初一数学新教材的意见，特向初中一年级400名学生作了问卷调查，并作出其条形统计图结果如下：
| 意见 |
非常喜欢 |
喜欢 |
有一点喜欢 |
不喜欢 |
| 频数 |
32 |
8 |
||
| 频率 |
0.5 |
0.4 |
（1）填表：计算出每一种意见的频数或频率；（填在答卷对应表格的空格中）
（2）请画出初中一年级400名学生的各种意见数的扇形统计图；
（3）从统计图中你能得出什么结论？说说你的理由．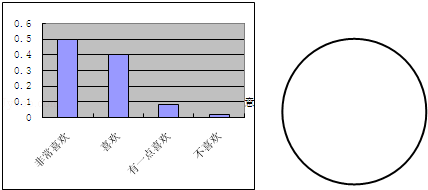
在抛硬1导致乘积减小最大币的实验中，某一小组的数据统计表如下所示，请将此表填写完整．
| 抛掷次数 |
100 |
250 |
500 |
… |
| 出现正面的频数 |
48 |
252 |
… |
|
| 出现正面的频率 |
51.6% |
… |