思考题:在对某地区的一次人口抽样统计分析中,各年龄段(年龄为整数)的人数如下表所示:
| 年龄段 |
0~9 |
10~19 |
20~29 |
30~39 |
40~49 |
50~59 |
60~69 |
70~79 |
80~89 |
| 人数 |
9 |
11 |
17 |
18 |
17 |
12 |
8 |
6 |
2 |
根据此表回答下列问题:
(1)样本中年龄在60岁以上(含60岁)的频率是 ;
(2)如果该地区现有人口80000人,为关注人口老龄化问题,请估算该地区60岁以上(含60岁)的人口数.
某工程队承包了某标段全长1755米的过江隧道施工任务,甲、乙两个班组分别从东、西两端同时掘进.已知甲组比乙组平均每天多掘进0.6米,经过5天施工,两组共掘进了45米.
(1)求甲、乙两个班组平均每天各掘进多少米?
(2)为加快工程进度,通过改进施工技术,在剩余的工程中,甲组平均每天能比原来多掘进0.2米,乙组平均每天能比原来多掘进0.3米.按此旄工进度,能够比原来少用多少天完成任务?
如图,在⊙O中,直径AB与弦CD相交于点P,∠CAB=40°,∠APD=65°。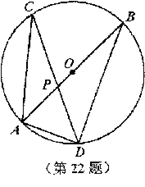
(1)求∠B的大小:
(2)已知圆心0到BD的距离为3,求AD的长。
“珍惜能源从我做起,节约用电人人有责”.为了解某小区居民节约用电情况,物业公司随机抽取了今年某一天本小区l0户居民的日用电量,数据如下:
| 用户序号 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| 日用电量(度) |
4.4 |
4.0 |
5.0 |
5.6 |
3.4 |
4.8 |
3.4 |
5.2 |
4.0 |
4.2 |
(1)求这组数据的极差和平均数;
(2)已知去年同一天这10户居民的平均日用电量为7.8度,请你估计,这天与去年同日相比,该小区200户居民这一天共节约了多少度电?
解不等式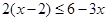 ,并写出它的正整数解。
,并写出它的正整数解。
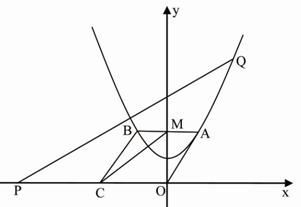
如图7,在平面直角坐标系xOy中,一抛物线的顶点坐标是(0,1),且过点(-2,2),平行四边形OABC的顶点A、B在此抛物线上,AB与y轴相交于点M.已知点C的坐标是(-4,0),点Q(x,y)是抛物线上任意一点.
(1)求此抛物线的解析式及点M的坐标;
(2)在x轴上有一点P(t,0),若PQ∥CM,试用x的代数式表示t;
(3)在抛物线上是否存在点Q,使得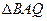 的面积是
的面积是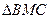 的面积的2倍?若存在,求
的面积的2倍?若存在,求
此时点Q的坐标.