如图7,在平面直角坐标系xOy中,一抛物线的顶点坐标是(0,1),且过点(-2,2),平行四边形OABC的顶点A、B在此抛物线上,AB与y轴相交于点M.已知点C的坐标是(-4,0),点Q(x,y)是抛物线上任意一点.
(1) 求此抛物线的解析式及点M的坐标;
(2) 在x轴上有一点P(t,0),若PQ∥CM,试用x的代数式表示t;
(3) 在抛物线上是否存在点Q,使得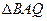 的面积是
的面积是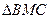 的面积的2倍?若存在,求
的面积的2倍?若存在,求
此时点Q的坐标.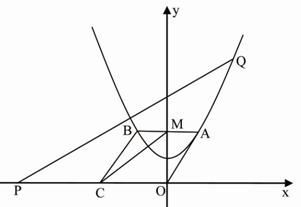
(本题7分)对于二次函数 ,如果当
,如果当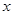 取任意整数时,
取任意整数时,
函数值 都是整数,此时称该点(
都是整数,此时称该点(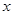 ,
, )为整点,该函数的图象为整点抛物线
)为整点,该函数的图象为整点抛物线
(例如: ).
).
(1)请你写出一个整点抛物线的解式.(不必证明);
(2)请直接写出整点抛物线
 与直线
与直线 围成的阴影图形中
围成的阴影图形中
(不包括边界)所含的整点个数.
(本题6分)已知:如图,△ABC是等边三角形,D是AB边上的点,将DB绕点D顺时针旋转60°得到线段DE,延长ED交AC于点F,连结DC、AE.
(1)求证:△ADE≌△DFC;
(2)过点E作EH∥DC交DB于点G,交BC于点H,连结AH.求∠AHE的度数;
(3)若BG=
 ,CH=2,求BC的长.
,CH=2,求BC的长.
(本题6分)列方程解应用题
某商店销售一种食用油,已知进价为每桶40元,市场调查发现,若以每桶50元的价格
销售,平均每天可以销售90桶油,若价格每升高1元,平均每天少销售3桶油,
设每桶食用油的售价为x元( ),商店每天销售这种食用油所获得的利润为y元.
),商店每天销售这种食用油所获得的利润为y元.(1)用含有x的代数式分别表示出每桶油的利润与每天卖出食用油的桶数;
(2)求y与x之间的函数关系式;
(3)当每桶食用油的价格为55元时,可获得多少利润?
(4)当每桶食用油的价格定为多少时,该商店一天销售这种食用油获得的利润最大?最大利润为多少?
(本题6分)已知关于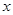 的方程
的方程 .
. (1)如果此方程有两个不相等的实数根,求m的取值范围;
(2)在(1)中,若m为符合条件的最大整数,求此时方程的根.
(本小题满分6分)
如图,在8×11的方格纸中,每个小正方形的边长均为1,△ABC的顶点均在小正方形的顶点处.
(1)画出△ABC绕点A顺时针方向旋转90°得到的△
 ;
;(2)求点B运动到点B′所经过的路径的长.