如图（1），（2）所示，矩形ABCD的边长AB＝6，BC＝4，点F在DC
上，DF＝2．动点M、N分别从点D、B同时出发，沿射线DA、线段BA向点A的方向运动（点M可运动到DA的延长线上），当动点N运动到点A时，M、N两点同时停止运动．连接FM、MN、FN，当F、N、M不在同一直线时，可得△FMN，过△FMN三边的中点作△PQW．设动点M、N的速度都是1个单位／秒，M、N运动的时间为x秒．试解答下列问题：DM=___▲____, AN=___▲____（用含x的代数式表示）
说明△FMN
∽ △QWP；试问
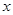为何值时，△PQW为直角三角形？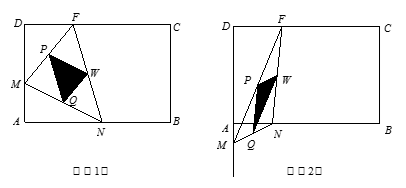 
问当
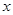为____▲_____时，线段MN最短？
将一副三角板中的两块直角三角尺的直角顶点C按如图方式叠放在一起：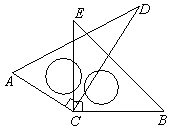
(1)若∠DCE＝35°，则∠ACB的度数为 ▲°；
(2)若∠ACB＝140°，则∠DCE的度数为 ▲°；
(3)∠ACB与∠DCE有怎样的数量关系?
(4)三角尺ACD不动，将三角尺BCE的CE边与CA边重合，然后绕点C按顺时针或逆时针方向任意转动一个角度，当∠ACE(0°＜∠ACE＜90°)等于多少度时，这两块三角尺各有一条边互相垂直，直接写出∠ACE角度所有可能的值，不用说明理由．
动点A从原点出发向数轴负方向运动，同时，动点B也从原点出发向数轴正方向运动，3s后，两点相距15cm(单位长度为1cm)．已知动点A、B的速度比是1∶4 (速度单位：cm/s)．
(1)求出3s后，A、B两点在数轴上对应的数分别是多少？
(2)若A、B两点从(1)中的位置同时向数轴负方向运动，经过几秒，原点恰好处在两个动点的正中间？
如图，下列几何体是由棱长为1的小立方体按一定规律在地面上摆成的，现将露出的表面都涂上颜色（下底面不涂色），则所给几何体中只有两个面涂色的小立方体的个数分别为：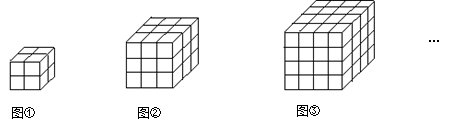
第1个几何体：最下面一层个数＝4；
第2个几何体：最下面一层个数+中间一层个数+最上面一层个数＝4+4+4＝12；
第3个几何体：最下面一层个数+中间两层个数+最上面一层个数＝4+8+8＝20；
……
总结规律，回答下列问题：
(1)第4个几何体中只有两个面涂色的小立方体共有 ▲个；
(2)第n个几何体中只有两个面涂色的小立方体共有多少个？（用含字母n的式子表示.）
生态公园计划在园内的坡地上种植甲、乙两种树，需要购买这两种树苗共100棵．甲种树苗的成活率为96%，乙种树苗的成活率为92%，若这批树苗种植后成活95棵，求购买甲、乙两种树苗各多少棵？
(1)由大小相同的小立方块搭成的几何体如图所示，请在方格中画出该几何体的俯视图和左视图
(2)用若干个大小相同的小立方体搭一几何体，使得它的俯视图和左视图与你上面所画的图一致，则这样的几何体最少要 ▲个小立方块，最多要 ▲个小立方块．