已知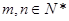 且
且 ,设
,设 ,
,  .(1)试求
.(1)试求 的系数的最小值;
的系数的最小值;
(2)对于使 的系数为最小的
的系数为最小的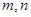 ,求此时
,求此时 的近似值(精确到0.01).
的近似值(精确到0.01).
如图,已知四棱锥 的底面ABCD为正方形,
的底面ABCD为正方形, 平面ABCD,E、F分别是BC,PC的中点,
平面ABCD,E、F分别是BC,PC的中点, ,
, .
.
(1)求证: 平面
平面 ;
;
(2)求二面角 的大小.
的大小.
如图, ,
, ,…,
,…, ,…是曲线
,…是曲线 上的点,
上的点, ,
, ,…,
,…, ,…是
,…是 轴正半轴上的点,且
轴正半轴上的点,且 ,
, ,…,
,…, ,… 均为斜边在
,… 均为斜边在 轴上的等腰直角三角形(
轴上的等腰直角三角形( 为坐标原点).
为坐标原点).
(1)写出 、
、 和
和 之间的等量关系,以及
之间的等量关系,以及 、
、 和
和 之间的等量关系;
之间的等量关系;
(2)求证: (
( );
);
(3)设 ,对所有
,对所有 ,
, 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
设椭圆 (常数
(常数 )的左右焦点分别为
)的左右焦点分别为 ,
, 是直线
是直线 上的两个动点,
上的两个动点, .
.
(1)若 ,求
,求 的值;
的值;
(2)求 的最小值.
的最小值.
一自来水厂用蓄水池通过管道向所管辖区域供水.某日凌晨,已知蓄水池有水9千吨,水厂计划在当日每小时向蓄水池注入水2千吨,且每 小时通过管道向所管辖区域供水
小时通过管道向所管辖区域供水 千吨.
千吨.
(1)多少小时后,蓄水池存水量最少?
(2)当蓄水池存水量少于3千吨时,供水就会出现紧张现象,那么当日出现这种情况的时间有多长?
已知函数 ,
, .
.
(1)设 是函数
是函数 的一个零点,求
的一个零点,求 的值;
的值;
(2)求函数 的单调递增区间.
的单调递增区间.