某迷宫有三个通道,进入迷宫的每个人都要经过一扇智能门。首次到达此门,系统会随机(即等可能)为你打开一个通道.若是1号通道,则需要1小时走出迷宫;若是2号、3号通道,则分别需要2小时、3小时返回智能门.再次到达智能门时,系统会随机打开一个你未到过的通道,直至走出迷宫为止.
(1)求走出迷宫时恰好用了1小时的概率;
(2)求走出迷宫的时间超过3小时的概率.
设
,
是
的反函数.
(Ⅰ)设关于
的方程求
在区间
上有实数解,求
的取值范围;
(Ⅱ)当
(e为自然对数的底数)时,证明:
;
(Ⅲ)当
时,试比较
与4的大小,并说明理由.
已知数列
满足a1=0,a2=2,且对任意
都有
(Ⅰ)求
;
(Ⅱ)设
,证明:
是等差数列;
(Ⅲ)设
,求数列
的前n项和
.
已知定点 ,定直线 : ,不在 轴上动点 与点 的距离是它到直线 的距离的2倍.设点 的轨迹为 ,过点 的直线交 于 两点,直线 分别交 于点
(Ⅰ)求
的方程;
(Ⅱ)试判断以线段
为直径的圆是否过点
,并说明理由.
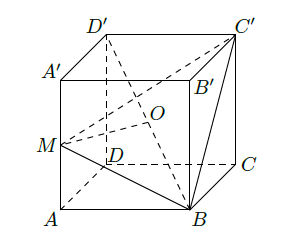
已知正方体
的棱长为1,点
是棱
的中点,点O是对角线
的中点.
(Ⅰ)求证:
为异面直线
和
的公垂线;
(Ⅱ)求二面角
的大小;
(Ⅲ)求三棱锥
的体积.