某化工厂拟建一座平面图形为矩形且面积为162平方米的三级污水处理池,池的深度一定(平面图如图所示).如果池四周围墙建造单价为400元/米,中间两道隔墙建造单价为248元/米,池底建造单价为80元/米2,水池所有墙的厚度忽略不计,试设计污水处理池的长和宽,使总造价最低,并求出最低总造价。
已知二次函数 的图象经过点
的图象经过点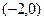 ,且不等式
,且不等式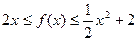 对一切实数
对一切实数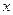 都成立.
都成立.
(1)求函数 的解析式;
的解析式;
(2)若对一切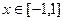 ,不等式
,不等式 恒成立,求实数
恒成立,求实数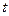 的取值范围.
的取值范围.
(本小题满 分13分)已知
分13分)已知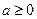 ,函数
,函数 .
.
(1)当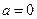 时讨论函数的单调性;
时讨论函数的单调性;
(2)当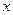 取何值时,
取何值时,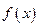 取最小值,证明你的结论.
取最小值,证明你的结论.
(本小题满分13分)已知函数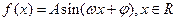 (其中
(其中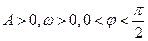 )的图象与x轴的交点中,相邻两个交点之间的距离为
)的图象与x轴的交点中,相邻两个交点之间的距离为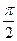 ,且图象
,且图象
上一个最低点 为
为 .
.
(1)求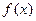 的解析式;
的解析式;
(2)当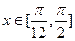 ,求
,求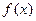 的值域.
的值域.
(本小题满分12分)
(1)判断函数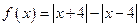 的奇偶性;
的奇偶性;
( 2)若
2)若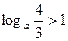 ,求a的取值范围.
,求a的取值范围.
(14分)某公司生产一种产品的固定成本为0.5万元,但每生产100件需再增加成本0.25万元,市场对此产品的年需求量为500件,年销售收入(单位:万元)为R(t)=5t- (0≤t≤5),其中t为产品售出的数量(单位:百件).
(0≤t≤5),其中t为产品售出的数量(单位:百件).
(1)把年利润表示为年产量x(百件)(x≥0)的函数f(x);
(2)当年产量为多少件时,公司可获得最大年利润?