某中学研究性学习小组,为了考察高中学生的作文水平与爱看课外书的关系,在本校高三年级随机调查了 50名学生.调査结果表明:在爱看课外书的25人中有18人作文水平好,另7人作文水平一般;在不爱看课外书的25人中有6人作文水平好,另19人作文水平一般.
(Ⅰ)试根据以上数据完成以下2×2列联表,并运用独立性检验思想,指出有多大把握认为中学生的作文水平与爱看课外书有关系?
高中学生的作文水平与爱看课外书的2×2列联表
| |
爱看课外书 |
不爱看课外书 |
总计 |
| 作文水平好 |
|
|
|
| 作文水平一般 |
|
|
|
| 总计 |
|
|
|
(Ⅱ)将其中某5名爱看课外书且作文水平好的学生分别编号为1、2、3、4、5,某5名爱看课外书且作文水平一般的学生也分别编号为1、2、3、4、5,从这两组学生中各任选1人进行学习交流,求被选取的两名学生的编号之和为3的倍数或4的倍数的概率.
参考公式: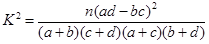 ,其中
,其中 .
.
参考数据:
 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
已知全集U=R,集合A={x|-1≤x<3},B={x|x-k≤0},
(1)若k="1," 求A∩CUB
(2) 若A∩B≠Æ,求k的取值范围
(本题 满分12分)已知
满分12分)已知 是椭圆
是椭圆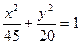 的两个焦点,
的两个焦点, 是椭圆上的点,且
是椭圆上的点,且 .
.
(1)求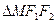 的周长;
的周长;
(2)求点 的坐标
的坐标
已知圆 ,点
,点 是圆内的任意一点,直线
是圆内的任意一点,直线 .
.
(1)求点 在第一象限的概率
在第一象限的概率 ;
;
(2)若 ,求直线
,求直线 与
与 圆
圆 相交的概率.
相交的概率.
(本小题满分12分)某中学生物兴趣小组在学校生物园地种植了一批名贵树苗,为了解树苗的生长情况,从这批树苗中随机地测量了其中50棵树苗的高度(单位:厘米),并把这些高度列成了如下的频数分布表:
(1)在这批树苗中任取,其高度在85厘米以上的大约有多少棵;
(2)这批树苗的平均 高度大约是多少?(计算时可以用组中值代替各组数据的平均值);
高度大约是多少?(计算时可以用组中值代替各组数据的平均值);
(3)为了进一步获得研究资料,若从 组中移出一棵树苗,从
组中移出一棵树苗,从 组中移出两棵树苗进行试验研究,则
组中移出两棵树苗进行试验研究,则 组中的树苗A和
组中的树苗A和 组中的树苗C同时被移出的概率是多少?
组中的树苗C同时被移出的概率是多少?
给出命题p:  ;命题q:曲线
;命题q:曲线 与
与 轴交于不同的两点.
轴交于不同的两点. 如果命题“
如果命题“ ”为真,“
”为真,“ ”为假,求实数
”为假,求实数 的取值范围.
的取值范围.