在△ABC中,已知B=45°,D是BC边上的一点,AD=10,AC=14,DC=6,
求⑴ ∠ADB的大小;⑵ BD的长.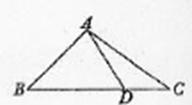
(本小题满分10分)函数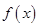 定义在R上的偶函数,当
定义在R上的偶函数,当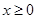 时,
时,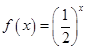
(1)写出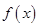 单调区间;
单调区间;
(2)函数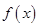 的值域;
的值域;
(本小题满分10分)已知函数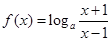 .
.
(1)求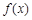 的定义域;(2)判断
的定义域;(2)判断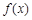 的奇偶性并证明;
的奇偶性并证明;
(本小题满分10分)已知函数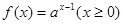 的图象经过点
的图象经过点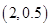 ,其中
,其中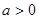 且
且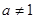 。
。
(1)求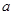 的值;
的值;
(2)求函数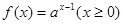 的值域。
的值域。
(本小题满分10分) 计算下列各式的值:
(1) ;
;
(2)
(本小题满分12分)
已知焦点在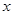 轴上的双曲线C的两条渐近线过坐标原点,且两条渐近线与以点
轴上的双曲线C的两条渐近线过坐标原点,且两条渐近线与以点 为圆心,1为半径的圆相切,又知C的一个焦点与A关于直线
为圆心,1为半径的圆相切,又知C的一个焦点与A关于直线 对称.
对称.
(1)求双曲线C的方程;
(2)设直线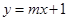 与双曲线C的左支交于A,B两点,另一直线
与双曲线C的左支交于A,B两点,另一直线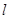 经过M(-2,0)及AB的中点,求直线
经过M(-2,0)及AB的中点,求直线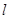 在
在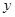 轴上的截距b的取值范围.
轴上的截距b的取值范围.