如图，抛物线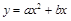
（a
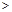0）与双曲线
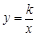相交于点A，B. 已知点A的坐标为（1，4），点B在第三象限内，且△AOB的面积为3（O为坐标原点）.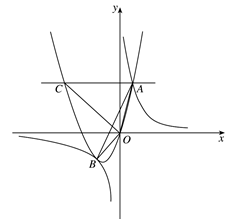
（1）求实数a，b，k的值；
（2）过抛物线上点A作直线AC∥x轴，交抛物线于另一点C，求所有满足△EOC∽△AOB的点E的坐标. （其中点E和点A，点C和点B分别是对应点）
先化简，再求值：（共4分）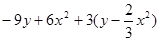
其中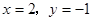
上海股民杨百万上星期五交易结束时买进某公司股票1000股，每股50 元，下表为本周内每日该股的涨跌情况 (星期六、日股市休市) (单位：元)
| 星期 |
一 |
二 |
三 |
四 |
五 |
| 每股涨跌 |
+4 |
+4.5 |
-1 |
2.5 |
-5 |
星期三收盘时，每股是多少元
本周内每股最高价多少元？最低价是多少元？
已知买进股票还要付成交金额2‰ 的手续费，卖出时还需付成交额2‰ 的手续费和1‰交易税，如果在星期五收盘前将全部股票卖出，他的收益情况如何？（注意：‰不是百分号，是千分号）
已知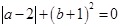
,求
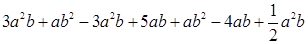的值
）如图，等腰梯形ABCD中，AB=4，CD=9，∠C=60°，动点P从点C出发沿CD方向向点D运动，动点Q同时以相同速度从点D出发沿DA方向向终点A运动，其中一个动点到达端点时，另一个动点也随之停止运动.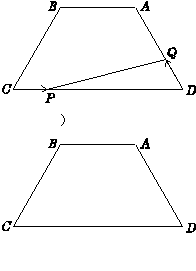
求AD的长；
设CP=x， △PDQ的面积为y,求y关于x的函数表达式， 并求自变量的取值范围
探究：在BC边上是否存在点M使得四边形PDQM是菱形？若存在，请找出点M，并求出BM的长；不存在，请说明理由.
如图，双曲线
上点A的坐标为（1，2），过点A的直线y=x+b交x轴于点M，交y轴于点N，过A作AP⊥x轴于点P。
分别求k、b的值；
求△AMP的周长。