某市组织20辆汽车装运食品、药品、生活用品三种救灾物资共100吨到灾民安置点.按计划20辆汽车都要装运,每辆汽车只能装运同一种救灾物资且必须装满,根据表中提供的信息,解答下列问题:
| 物资种类 |
食品 |
药品 |
生活用品 |
| 每辆汽车装载量(吨) |
6 |
5 |
4 |
| 每吨所需运费(元/吨) |
120 |
160 |
100 |
(1)设装运食品的车辆数为x,装运药品的车辆数为y,求y与x的函数关系式;
(2)如果装运食品和装运药品的车辆数均不少于4辆,求装运食品的车辆数x的取值范围;
(3)在(2)的条件下,若要求总运费最少,应如何安排车辆?并求出最少总运费.
如图,平面直角坐标系中,O为坐标原点,等腰梯形ABCD四个顶点都在抛物线y=ax2+bx+c上,其中点A、B在x轴上,点D在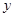 轴上,且CD∥AB, 已知S梯形ABCD=8,tan∠DAO=4,点B的坐标为(2,0),点E坐标为(0,-1).
轴上,且CD∥AB, 已知S梯形ABCD=8,tan∠DAO=4,点B的坐标为(2,0),点E坐标为(0,-1).
(1)求此抛物线的解析式;
(2)若△OEB从点B开始以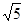 个单位每秒的速度沿BD向终点D匀速运动. 设运动时间为t秒,在整个运动过程中,当边OE与线段AD相交时,求运动时间t的取值范围;
个单位每秒的速度沿BD向终点D匀速运动. 设运动时间为t秒,在整个运动过程中,当边OE与线段AD相交时,求运动时间t的取值范围;
(3)能否将△OEB绕平面内某点旋转90°后使得△OEB的两个顶点落在x轴上方的抛物线上,若能,请直接写出旋转中心的坐标,若不能,请说明理由.
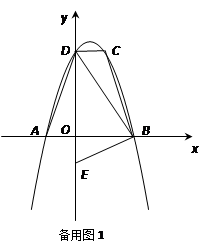

如图,边长为4的等边△AOB的顶点O在坐标原点,点A在x轴正半轴上,点B在第一象限.一动点P沿x轴以每秒1个单位长度的速度由点O向点A匀速运动,当点P到达点A时停止运动,设点P运动的时间是t秒.在点P的运动过程中,线段BP的中点为点E,将线段PE绕点P按顺时针方向旋转60º得PC.
(1)当点P运动到线段OA的中点时, 点C的坐标为 ;
(2)在点P从点O到点A的运动过程中,用含t的代数式表示点C的坐标;
(3)在点P从点O到点A的运动过程中,求出点C所经过的路径长.
在日常生活中,我们经常有目的地收集数据,分析数据,作出预测.
(1)下图是小芳家2011年全年月用电量的条形统计图. 根据图中提供的信息,回答下列问题:
①2011年小芳家月用电量最小的是月,四个季度中用电量最大的是第季度;
②求2011年5月至6月用电量的月增长率;
(2)今年小芳家添置了新电器.已知今年5月份的用电量是120千瓦时,根据2011年5月至7月用电量的增长趋势,预计今年7月份的用电量将达到240千瓦时.假设今年5月至6月用电量月增长率是6月至7月用电量月增长率的1.5倍,预计小芳家今年6月份的用电
量是多少千瓦时?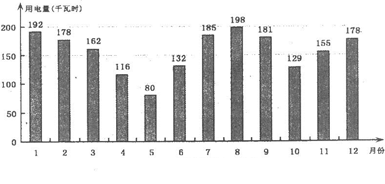
如图,⊙O的弦AD∥BC,过点D的切线交BC的延长线于点E,AC∥DE交BD于点H,DO及延长线分别交AC、BC于点G、F.
(1)求证:DF垂直平分AC;
(2)求证:FC=CE;
(3)若弦AD=5㎝,AC=8㎝,求⊙O的半径.
如图,某数学课外活动小组测量电视塔AB的高度,他们借助一个高度为30m的建筑物CD进行测量,在点C处塔顶B的仰角为45°,在点E处测得B的仰角为37°(B、D、E三点在一条直线上).求电视塔的高度h.(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)