某批发商以每件50元的价格购进800件衬衣,第一个月以单价80元销售,售出了200件;第二个月如果单价不变,预计可售出200件,批发商为增加销售,决定降价销售,根据市场调查,单价每降低1元,可多售出10件,但最低单价应高于购进的价格;第二个月结束后,批发商将对剩余的衬衣一次性清仓销售,清仓时单价为40元,设第二个月单价降低x元.填写下表
| 时间 |
第一个月 |
第二个月 |
清仓时 |
| 单价(元) |
80 |
40 |
|
| 销量(件) |
200 |
|
|
如果批发商销售这批衬衣后获利9000元,求第二个月的单价是多少?
如图,在□ABCD中,E、F为BC上的两点,且BE=CF,AF=DE.
求证:(1)△ABF≌△DCE;
(2)四边形ABCD是矩形.
解方程: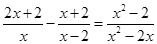
计算
(1)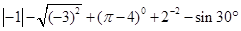
(2)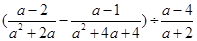 ,其中a满足
,其中a满足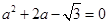
如图1所示,将一个边长为2的正方形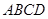 和一个长为2、宽为1的长方形
和一个长为2、宽为1的长方形 拼在一起,构成一个大的长方形
拼在一起,构成一个大的长方形 .现将小长方形
.现将小长方形 绕点
绕点 顺时针旋转至
顺时针旋转至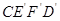 ,旋转角为
,旋转角为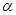 .
.
(1)当点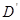 恰好落在
恰好落在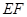 边上时,求旋转角
边上时,求旋转角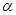 的值;
的值;
(2)如图2,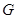 为
为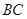 的中点,且0°<
的中点,且0°<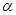 <90°,求证:
<90°,求证: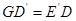 ;
;
(3)先将小长方形 绕点
绕点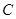 顺时针旋转,使
顺时针旋转,使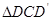 与
与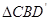 全等(0°<
全等(0°<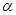 <180°),再将此时的小长方形
<180°),再将此时的小长方形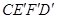 沿CD边竖直向上平移t个单位,设移动后小长方形边直线
沿CD边竖直向上平移t个单位,设移动后小长方形边直线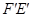 与BC交于点H,若DH∥FC,求上述运动变换过程中
与BC交于点H,若DH∥FC,求上述运动变换过程中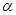 和t的值.
和t的值.
函数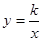 和
和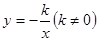 的图象关于y轴对称,我们定义函数
的图象关于y轴对称,我们定义函数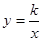 和
和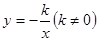 相互为“影像”函数。
相互为“影像”函数。
类似地,如果函数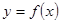 和
和 的图象关于y轴对称,那么我们定义函数
的图象关于y轴对称,那么我们定义函数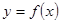 和
和 互为“影像”函数。
互为“影像”函数。
(1)请写出函数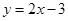 的“影像”函数:;
的“影像”函数:;
(2)函数的“影像”函数是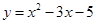 ;
;
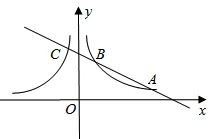
(3)如果,一条直线与一对“影像”函数 和
和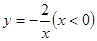 的图象分别交于点A、B、C(点A、B在第一象限),如果CB: BA=1:2,点C在函数
的图象分别交于点A、B、C(点A、B在第一象限),如果CB: BA=1:2,点C在函数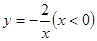 的“影像”函数上的对应点的横坐标是1,求点B的坐标。
的“影像”函数上的对应点的横坐标是1,求点B的坐标。