某企业获准生产“上海世博会”纪念徽章,若生产A种款式的纪念徽章125件,B种款式的纪念徽章150件,需生产成本700元;若生产A种款式的纪念徽章100件,B种款式的纪念徽章450件,需生产成本1550元.已知A、B两种纪念徽章的市场零售价分别为2.3元,3.5元求每个A、B两种款式的纪念徽章的成本是多少元?
随着上海世博会的开幕,为了满足市场的需要,该企业现在每天要生产A、B两种款式的纪念徽章共4500件,若要求每天投入成本不超过10000元,并且每天生产的B种款式的纪念徽章不少于A种款式纪念徽章的
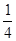 .那么每天最多获利多少元,最少获利多少元?获利最多的方案如何设计?
.那么每天最多获利多少元,最少获利多少元?获利最多的方案如何设计?
定义新运算:对于任意实数a,b,都有a⊕b=a(a﹣b)+1,等式右边是通常的加法、减法及乘法运算,比如:2⊕5=2×(2﹣5)+1=2×(﹣3)+1=﹣6+1=﹣5
(1)求(﹣2)⊕3的值;
(2)若3⊕x的值小于13,求x的取值范围,并在图所示的数轴上表示出来.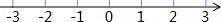
如图,抛物线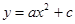 经过
经过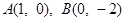 两点.连结
两点.连结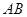 ,过点
,过点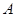 作
作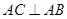 ,交抛物线于点
,交抛物线于点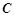 .
.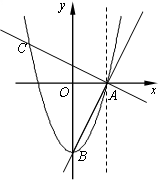
(1)求该抛物线的解析式;
(2)求点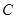 的坐标;
的坐标;
(3)将抛物线沿着过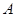 点且垂直于
点且垂直于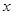 轴的直线对折,再向上平移到某个位置后此抛物线与直线
轴的直线对折,再向上平移到某个位置后此抛物线与直线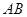 只有一个交点,请直接写出此交点的坐标.
只有一个交点,请直接写出此交点的坐标.
如图,已知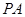 、
、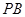 是⊙
是⊙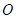 的切线,
的切线,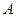 、
、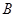 为切点.直径
为切点.直径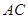 的延长线与
的延长线与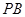 的延长线交于点
的延长线交于点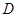 .
.
(1)求证: ;
;
(2)若 ,
,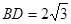 .求图中阴影部分的面积(结果保留根号与
.求图中阴影部分的面积(结果保留根号与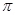 ).
).
为迎接2014年世界杯足球赛,某商家购进甲、乙两种纪念品.甲种纪念品的进货价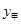 (元/件)与进货数量
(元/件)与进货数量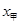 (件)的关系如图所示.
(件)的关系如图所示. 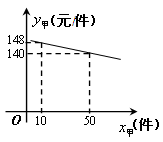
(1)求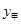 与
与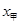 的关系式;
的关系式;
(2)若商家购进甲种纪念品的数量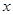 不少于
不少于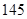 件,且甲种纪念品的进货价不低于
件,且甲种纪念品的进货价不低于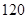 元/件,则该商家有几种进货方案?
元/件,则该商家有几种进货方案?
(3)该商家若购进甲、乙两种纪念品共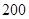 件,其中乙种纪念品的进货价
件,其中乙种纪念品的进货价 (元/件)与进货数量
(元/件)与进货数量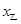 (件)满足关系式
(件)满足关系式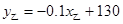 .商家分别以
.商家分别以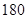 元/件、
元/件、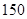 元/件出售甲、乙两种纪念品,并且全部售完.在(2)的条件下,购进甲种纪念品多少件时,所获总利润最大?最大利润是多少?(说明:本题不要求写出自变量
元/件出售甲、乙两种纪念品,并且全部售完.在(2)的条件下,购进甲种纪念品多少件时,所获总利润最大?最大利润是多少?(说明:本题不要求写出自变量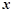 的取值范围)
的取值范围)
如图,某校一大楼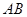 的高为
的高为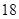 米,不远处有一水塔
米,不远处有一水塔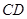 .某同学在楼底
.某同学在楼底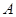 处测得塔顶
处测得塔顶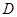 处的仰角为
处的仰角为 ,在楼顶
,在楼顶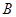 点测得塔顶
点测得塔顶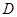 处的仰角为
处的仰角为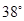 .求
.求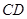 的高度(结果精确到
的高度(结果精确到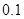 米) .(参考数据:
米) .(参考数据: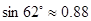 ,
,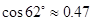 ,
,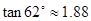 ,
,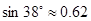 ,
,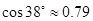 ,)
,)