已知抛物线 经过
经过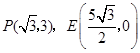 及原点
及原点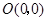 .
.求抛物线的解析式.
过
 点作平行于
点作平行于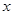 轴的直线
轴的直线 交
交 轴于
轴于 点,在抛物线对称轴右侧且位于直线
点,在抛物线对称轴右侧且位于直线 下方的抛物线上,任取一点
下方的抛物线上,任取一点 ,过点
,过点 作直线
作直线 平行于
平行于 轴交
轴交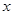 轴于
轴于 点,交直线
点,交直线 于
于 点,直线
点,直线 与直线
与直线 及两坐标轴围成矩形
及两坐标轴围成矩形 (如图).是否存在点
(如图).是否存在点 ,使得
,使得 与
与 相似?若存在,求出
相似?若存在,求出 点的坐标;若不存在,请说明理由
点的坐标;若不存在,请说明理由如果符合(2)中的
 点在
点在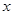 轴的上方,连结
轴的上方,连结 ,矩形
,矩形 内的四个三角形
内的四个三角形 之间存在怎样的关系?为什么?
之间存在怎样的关系?为什么?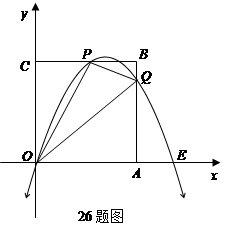
如图,一次函数 与反比例函数 的图象在第二象限交于点 ,且点 的横坐标为 .
(1)求反比例函数的解析式;
(2)点 的坐标是 ,若点 在 轴上,且 的面积与 的面积相等,求点 的坐标.

据《德阳县志》记载,德阳钟鼓楼始建于明朝成化年间,明末因兵灾焚毁,清乾隆五十二年重建.在没有高层建筑的时代,德阳钟鼓楼一直流传着“半截还在云里头”的故事.1971年,因破四旧再次遭废.现在的钟鼓楼是老钟鼓楼的仿制品,于2005年12月27日破土动工,2007年元旦落成,坐落东山之巅,百尺高楼金碧辉煌,流光溢彩;万丈青壁之间,银光闪烁,蔚为壮观,已经成为人们休闲的打卡胜地.
学校数学兴趣小组在开展“数学与传承”探究活动中,进行了“钟鼓楼知识知多少”专题调查活动,将调查问题设置为“非常了解”、“比较了解”、“基本了解”、“不太了解”四类.他们随机抽取部分市民进行问卷调查,并将结果绘制成了如下两幅统计图:
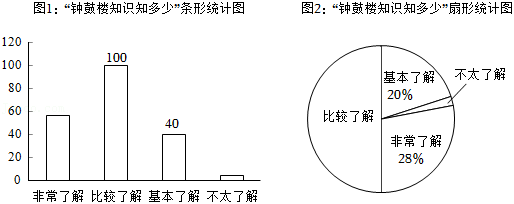
(1)设本次问卷调查共抽取了 名市民,图2中“不太了解”所对应扇形的圆心角是 度,分别写出 的值;
(2)根据以上调查结果,在 名市民中,估计“非常了解”的人数有多少?
(3)为进一步跟踪调查市民对钟鼓楼知识掌握的具体情况,兴趣组准备从附近的 名男士和 名女士中随机抽取 人进行调查,请用列举法(树状图或列表)求恰好抽到一男一女的概率.
计算: .
如图1,在平面直角坐标系中,抛物线 与x轴交于A, 两点,点C在y轴上,且 ,D,E分别是线段AC,AB上的动点(点D,E不与点A,B,C重合).
(1)求此抛物线的表达式;
(2)连接DE并延长交抛物线于点P,当 轴,且 时,求DP的长;
(3)连接BD.
①如图2,将△BCD沿x轴翻折得到△BFG,当点G在抛物线上时,求点G的坐标;
②如图3,连接CE,当 时,求 的最小值.

已知正方形ABCD,E为对角线AC上一点.
【建立模型】
(1)如图1,连接BE,DE.求证: ;
【模型应用】
(2)如图2,F是DE延长线上一点, ,EF交AB于点G.
①判断△FBG的形状并说明理由;
②若G为AB的中点,且AB=4,求AF的长.
【模型迁移】
(3)如图3,F是DE延长线上一点, ,EF交AB于点G, .求证: .
