某厂家新开发的一种摩托车如图所示，它的大灯A射出的光线AB、AC与地面
MN的夹角分别为8°和10°，大灯A离地面距离1 m．该车大灯照亮地面的宽度BC约是多少（不考虑其它因素）？
一般正常人从发现危险到做出刹车动作的反应时间是0.2 s，从发现危险到摩托
车完全停下所行驶的距离叫做最小安全距离，某人以60 km/h的速度驾驶该车，从60 km/h
到摩托车停止的刹车距离是
m，请判断该车大灯的设计是否能满足最小安全距离的要求，
请说明理由．（不考虑车轮的长度）
（参考数据：sin8°≈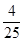
，tan8°≈
，sin10°≈
，tan10°≈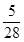
）
如图，∠ABC的平分线BF与△ABC中∠ACB的相邻外角的平分线CF相交于点F，过F作DF∥BC，交AB于D，交AC于E．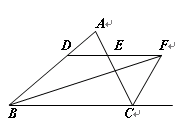
（1）试说明BD＝DF；
（2）请写出图中所有的等腰三角形；
（3）线段BD，CE，DE之间存在怎样的数量关系？请说明理由．
如图，在等腰△ABC中，CH是底边上的高线，点P是线段CH上不与端点重合的任意一点，连结AP交BC于点E，连结BP交AC于点F.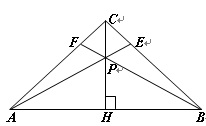
（1）试说明∠CAE＝∠CBF；
（2）AE和BF 是否相等？请说明理由.
如图，已知AB∥CD，∠1＝40º，∠2＝70º，求出∠3，∠4的度数.
如图，在△ABC中，AB＝AC，D，E分别是AB，AC的中点.
（1）试说明BE＝CD；
（2）请用一句话叙述由第（1）小题得出的结论.
如图，已知EF∥AD，∠1 ＝∠2，∠BAC＝65º．请将求∠AGD的过程填写完整．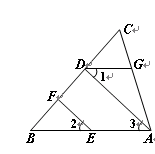
解：∵EF∥AD（）
∴∠2＝ （）
又∵∠1＝∠2
∴∠1＝∠3（）
∴AB∥ （）
∴∠BAC＋ ＝180º．
又∵∠BAC＝65º
∴∠AGD＝ ．