2011年,陕西西安被教育部列为“减负”工作改革试点地区。学生的学业负担过重会严重影响学生对待学习的态度.为此西安市教育部门对部分学校的八年级学生对待学习的态度进行了一次抽样调查(把学习态度分为三个层级,A级:对学习很感兴趣;B级:对学习较感兴趣;C级:对学习不感兴趣),并将调查结果绘制成图①和图②的统计图(不完整).请根据图中提供的信息,解答下列问题:此次抽样调查中,共调查了 名学生;
将图①补充完整;
求出图②中C级所占的圆心角的度数;
根据抽样调查结果,请你估计我市近80000名八年级学生中大约有多少名学生学习态度达标(达标包括A级和B级)?

(本题14分)如图,AB为⊙O的直径,AC为⊙O的弦,AD平分∠BAC,交⊙O于点D,DE⊥AC,交AC的延长线于点E.
(1)判断直线DE与⊙O的位置关系,并说明理由;
(2)若AE=8,⊙O的半径为5,求DE的长.
(本题12分)△ABC在直角坐标系中的位置如图所示,直线l经过点(-1,0),并且与y轴平行. 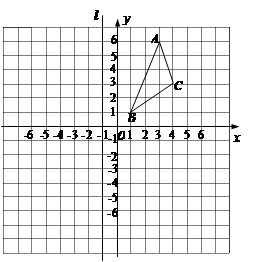
(1)①将△ABC绕坐标原点O顺时针旋转90°得到△A1B1C1,在图中画出△A1B1C1;
②求出由点C运动到点C1所经过的路径的长.
(2)①△A2B2C2与△ABC关于直线l对称,画出△A2B2C2,并写出△A2B2C2三个顶点的坐标;
②观察△ABC与△A2B2C2对应点坐标之间的关系,写出直角坐标系中任意一点P(a,b)关于原点O的对称点M的坐标:____ ______.
(本题10分)如图,AB为⊙O直径,BC切⊙O于B,CO交⊙O交于D,AD的延长线交BC于E,若∠C = 25°,求∠A的度数。
(本题10分)如图,AB是⊙O的直径,BC是弦,OD⊥BC于E,交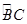 于D.
于D.
(1)请写出四个不同类型的正确结论;
(2)若BC = 8,ED = 2,求⊙O的半径.
(本题8分)某商店将进价为8元的商品按每件10元售出,每天可售出200件,现在采取提高商品售价减少销售量的办法增加利润,如果这种商品每件的销售价每提高0.5元其销售量就减少10件,问应将每件售价定为多少元时,才能使每天利润为640元?