（本题12分）△ABC在直角坐标系中的位置如图所示，直线l经过点（-1，0），并且与y轴平行．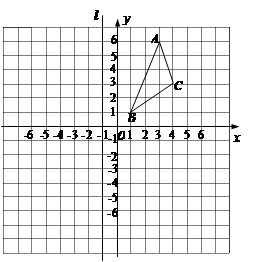 
（1）①将△ABC绕坐标原点O顺时针旋转90°得到△A1B1C1，在图中画出△A1B1C1；
②求出由点C运动到点C1所经过的路径的长．
（2）①△A2B2C2与△ABC关于直线l对称，画出△A2B2C2，并写出△A2B2C2三个顶点的坐标；
②观察△ABC与△A2B2C2对应点坐标之间的关系，写出直角坐标系中任意一点P（a，b）关于原点O的对称点M的坐标：____ ______．
先化简，再求值：（1+
）•
，其中x=
+1．
如图，已知AB是⊙O的直径，AB=8， 点C在半径OA上（点C与点O、A不重合），过点C作AB的垂线交⊙O于点D，连结OD，过点B作OD的平行线交⊙O于点E、交射线CD于点F．
（1）若
，求∠F的度数；
（2）设
写出
与
之间的函数解析式，并写出自变量取值范围；
（3）设点C关于直线OD的对称点为P，若△PBE为等腰三角形，求OC的长．
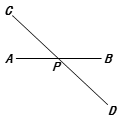
如果有两点到一条直线的距离相等，那么称这条直线为 “两点的等距线”．
|
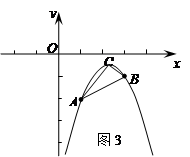
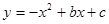过点
（，
），
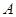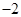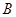（3，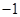
），顶点为C．抛物线上是否存在点P ,使
，若存在，求出点P的坐标；若不存在，请说明理由。
宁波某水果店计划购进甲、乙两种新出产的水果共140千克，这两种水果的进价、售价如表所示：
| 进价（元/千克） |
售价（元/千克） |
|
| 甲种 |
5 |
8 |
| 乙种 |
9 |
13 |
（1）若该水果店预计进货款为1000元，则这两种水果各购进多少千克？
（2）若该水果店决定乙种水果的进货量不超过甲种水果的进货量的3倍，应怎样安排进货才能使水果点在销售完这批水果时获利最多？此时利润为多少元？
如图，在Rt△ABC中，∠ACB=90°，以AC为直径的⊙O与AB边交于点D，过点D的切线，交BC于点E．
（1）求证：EB=EC；
（2）若以点O、D、E、C为顶点的四边形是正方形，试判断△ABC的形状，并说明理由．