在△ABC中，∠ACB＝90°，∠ABC＝30°，将△ABC绕顶点C顺时针旋转，旋转角为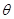
(0°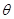＜＜180°)，得到△A1B1C．
如图1，当AB∥CB1时，设A1B1与BC相交于点D．证明：△A1CD是等边三角形；
如图2，连接AA1、BB1，若△ACA1的面积为S，求△BCB1的面积
如图3，设AC的中点为E，A1B1的中点为P，AC＝a，连接EP．求EP的长度最大时∠
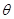的度数，并求出此时EP的最大值．
（本题满分l2分）⊙O直径AB=4，∠ABC=30°，BC=4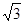
。D是线段BC中点，
（1）试判断D与⊙O的位置关系并说明理由；
（2）过点D作DE⊥AC，垂足为E，求证：直线DE是⊙O切线。
某超市的某种商品现在的售价为每件50元，每周可以卖出500件。现市场调查反映：如果调整价格，每涨价1元，每周要少卖出10件。已知该种商品的进价为每件40元，问如何定价，才能使利润最大?最大利润是多少?（每件商品的利润=售价－进价）
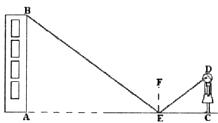
小玲用下面的方法来测量学校教学大楼AB的高度：如图，在水平地面上放一面平面镜，镜子与教学大楼的距离EA=21米．当她与镜子的距离CE=2．5米时，她刚好能从镜子中看到教学大楼的顶端B．已知她的眼睛距地面高度DC=1．6米．请你帮助小玲计算出教学大楼的高度AB是多少米（注意：根据光的反射定律：反射角等于入射角）．