(本小题满分13分)
(1)操作发现:如图①,D是等边△ABC边BA上一动点(点D与点B不重合),连接DC,以DC为边在BC上方作等边△DCF,连接AF.直接写出线段AF与BD之间的数量关系.
(2)类比猜想:如图②,当△ABC为以BC为斜边的等腰直角三角形,D是△ABC边BA上一动点(点D 与点B不重合),连接DC,以DC为斜边在BC上方作等腰直角△FDC,连接AF.请直接写出它们的数量关系.
(3)深入探究:
Ⅰ.如图③,当△ABC为以BC为底边的等腰三角形,D是△ABC边BA上一动点(点D与点B不重合),连接DC,以DC为底边在BC上方作等腰△FDC,∠BC A=∠DCF,且∠B A C =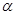 ,连接AF.线段AF与BD之间的有什么数量关系?证明你发现的结论;
,连接AF.线段AF与BD之间的有什么数量关系?证明你发现的结论;
Ⅱ.如图④,当△ABC为任意三角形,D是△ABC边BA上一动点(点D与点B不重合),连接DC,以DC为边在BC上方作△FDC∽△ABC,且 ,连接AF.线段AF与BD之间的有什么数量关系?直接写出你发现的结论.
,连接AF.线段AF与BD之间的有什么数量关系?直接写出你发现的结论.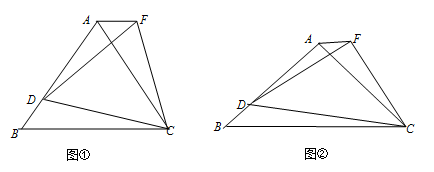

某校七年级的三个班一起去打草,一班打草600千克,二班比一班多打草150千克,三班比二班少打100千克,把二,三班的草按照9:11分给一队和二队,各队应分多少千克?
世界上最高的山峰是珠穆朗玛峰,其海拔高度是8844M,吐鲁番盆地的海拔高度大约是-155M。两处高度相差多少米﹖
下图是由几个小立方块所搭几何体的俯视图,小正方形中的数字表示在该位置的小立方体的个数。请画出这个几何体的主视图、左视图。
认真画出下面物体的主视图.
(本题满分8分)已知OC是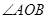 内部的一条射线,M、N分别为OA、OC上的点,线段OM、ON分别以30°/s、10°/s的速度绕点O逆时针旋转。
内部的一条射线,M、N分别为OA、OC上的点,线段OM、ON分别以30°/s、10°/s的速度绕点O逆时针旋转。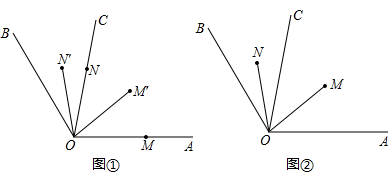

(1)如图①,若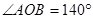 ,当OM、ON逆时针旋转2s时,分别到OM′、ON′处,求
,当OM、ON逆时针旋转2s时,分别到OM′、ON′处,求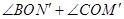 的值;
的值;
(2)如图②,若OM、ON分别在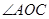 、
、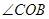 内部旋转时,总有
内部旋转时,总有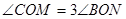 ,求
,求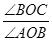 的值.
的值.
(3)知识迁移,如图③,C是线段AB上的一点,点M从点A出发在线段AC上向C点运动,点N从点C出发在线段CB上向B点运动,点M、N的速度比是2:1,在运动过程中始终有CM=2BN,求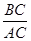 =.
=.