已知各项均为正数的两个数列{an}和{bn}满足：an1an-优题课

题文

已知各项均为正数的两个数列 ${a_{n}}$ 和 ${b_{n}}$ 满足： $a_{n + 1} = \frac{a_{n} + b_{n}}{\sqrt{{a_{n}}^{2} + {b_{n}}^{2}}}, n \in N^{*}$ ，
（1）设 $b_{n + 1} = 1 + \frac{b_{n}}{a_{n}}, n \in N^{*}$ ，求证：数列 ${(\frac{b_{n}}{a_{n}})^{2}}$ 是等差数列；

（2）设 $b_{n + 1} = \sqrt{2} \cdot \frac{b_{n}}{a_{n}}, n \in N^{*}$ ，且 ${a_{n}}$ 是等比数列，求 $a_{1}$ 和 $b_{1}$ 的值．

科目数学题型解答题难度中等

登录免费查看答案和解析

相关试题

（本小题14分）设函数,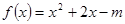
（1）当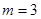时，求函数f（x）的零点；
（2）当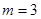时，判断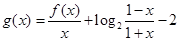的奇偶性并给予证明；
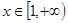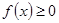（3）当时，恒成立，求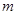的最大值．

（本小题满分14分）某租凭公司拥有汽车100辆，当每辆汽车的月租为3000元时，可全部租出，当每辆车的月租金增加50元时，未租出的车辆会增加一辆，租出的车每辆每月需要维护费150元，未租出的车每月需要维护费50元。
（1）当每辆车的月租金定位3600时，能租出多少辆车？
（2）当每辆车的月租金定位多少钱时，租凭公司的月收益最大？最大收益是多少？

（本小题满分14分）已知函数的图像如图所示，

（1）求的解析式；
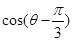（2）若，，求的值．

（本小题满分14分）已知
（1）求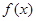的最小正周期及；
（2）求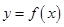的单调增区间；
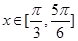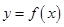（3）当时，求的值域．

（本小题满分12分）已知，
（1）求及；
（2）求的值．

试卷网试题网古诗词网作文网范文网

Copyright ©2020-2025 优题课 youtike.com 版权所有

粤ICP备20024846号