如图,在矩形ABCD中,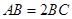 ,
,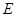 为
为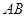 上一点,以直线EC为折线将点B折起至点P,并保持∠PEB为锐角,连结PA、PC、PD,取PD的中点F,若有AF∥平面PEC。
上一点,以直线EC为折线将点B折起至点P,并保持∠PEB为锐角,连结PA、PC、PD,取PD的中点F,若有AF∥平面PEC。
(Ⅰ)试确定点E的位置;
(Ⅱ)若异面直线PE、CD所成的角为60°,求证:平面PEC⊥平面AECD。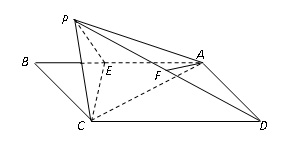
在△ABC中, 分别为角A、B、C的对边,
分别为角A、B、C的对边,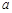 =3,△ABC的面积为6,
=3,△ABC的面积为6, ,D为△ABC内任一点,点D到三边距离之和为
,D为△ABC内任一点,点D到三边距离之和为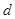 。
。
(1)求:角A的正弦值;
(2)求:边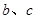 ;
;
(3)求: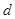 的取值范围
的取值范围
已知正项等差数列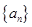 的前
的前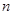 项和为
项和为 ,若
,若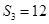 ,且
,且 成等比数列.
成等比数列.
(Ⅰ)求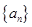 的通项公式;
的通项公式;
(Ⅱ)记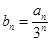 的前
的前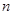 项和为
项和为 ,求
,求 .
.
如图,设 是单位圆和
是单位圆和 轴正半轴的交点,
轴正半轴的交点, 是单位圆上的两点,
是单位圆上的两点, 是坐标原点,
是坐标原点, ,
, .
.
(1)若 ,求
,求 的值;
的值;
(2)设函数 ,求
,求 的值域.
的值域.
在等比数列{ }中,
}中, ,公比
,公比 ,且
,且 ,
,  与
与 的等比中项为2.
的等比中项为2.
(1)求数列{ }的通项公式;
}的通项公式;
(2)设 ,求:数列{
,求:数列{ }的前
}的前 项和为
项和为 ,
,
设函数 ,
, .
.
(1)当 时,函数
时,函数 取得极值,求
取得极值,求 的值;
的值;
(2)当 时,求函数
时,求函数 在区间[1,2]上的最大值;
在区间[1,2]上的最大值;
(3)当 时,关于
时,关于 的方程
的方程
 有唯一实数解,求实数
有唯一实数解,求实数 的值.
的值.