如图，在直角坐标系中，⊙O的圆心O在坐标原点，直径AB=8，点P是直径AB上的一个动点（点P不与A、B两点重合），过点P的直线PQ的解析式为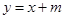
，当直线PQ交y轴于Q，交⊙O于C、D两点时，过点C作CE垂直于x轴交⊙O于点E，过点E作EG垂直于y轴，垂足为G，过点C作CF垂直于y轴，垂足为F，连接DE．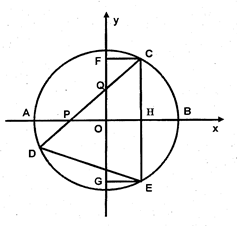
（1）点P在运动过程中，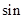
∠CPB= ；
（2）当m=3时，试求矩形CEGF的面积；
（3）当P在运动过程中，探索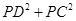
的值是否会发生变化？如果发生变化，请你说明理由；如果不发生变化，请你求出这个不变的值；
（4）如果点P在射线AB上运动，当△PDE的面积为4时，请你求出CD的长度
(1)由图中提供信息：乒乓球、排球、足球、篮球4项球类活动中，哪一类球类运动能够获得全班近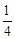
的支持率?
(2)若全班人数为50人，体育委员组织一次排球比赛，估计会有多少人积极参加比赛?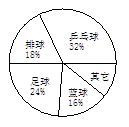
全班约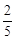
是男生，约
是女生，请根据所给数据完成扇形统计图.
某人将20000元钱分成两部分，按两种不同方式存入银行，其中10000元按活期方式存一年，另10000元按定期存一年，一年后共取回21044元，又已知定期一年存款约利率为0.63％，求活期存款月利率是多少？
肖青的妈妈前年买了某公司的二年期债券4500元，今年到期，扣除利息税后，共得本利和约4700元，问这种债券的年利率是多少？（精确到0.01％）
教育储蓄年利率为1.98％，免征利息税，某企业发行的债券月利率为2.15‰，但要征收20％的利息税，为获取更大回报，投资者应选择哪一种储蓄呢？某人存入28000元，一年到期后可以多收益多少元？