如图,从顶点A出发,沿着边长为1的正方形的四个顶点依次跳舞,舞步长为1.第一次顺时针移动1步,第二次逆时针移动2步,第三次顺时针移动3步,……以此类推.
(1)移动4次后到达何处?(直接给出答案)
(2)移动2012次后到达何处?
进入防汛期后,某地对河堤进行了加固.该地驻军在河堤加固的工程中出色完成了任务.这是记者与驻军工程指挥官的一段对话:
通过这段对话,请你求出该地驻军原来每天加固的米数.
如图,在一次数学课外活动中,小明同学在点P处测得教学楼A位于北偏东60°方向,办公楼B位于南偏东45°方向.小明沿正东方向前进60米到达C处,此时测得教学楼A恰好位于正北方向,办公楼B正好位于正南方向.求教学楼A与办公楼B之间的距离(结果精确到0.1米).
(供选用的数据: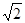 ≈1.414,
≈1.414,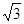 ≈1.732)
≈1.732)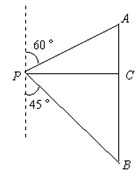
“一方有难,八方支援”,在四川汶川大地震后,某市文华中学全体师生踊跃捐款,向灾区人民献爱心. 为了了解该校学生捐款情况,对其中60个学生捐款数x(元)分五组进行统计,第一组:1≤x≤5,第二组:6≤x≤10,第三组:11≤x≤15,第四组:16≤x≤20;,第五组:x≥21,并绘制如下频数分布直方图(假定每名学生捐款数均为整数),解答下列问题: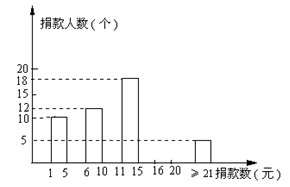
(1) 补全频数分布直方图;
(2) 这60个学生捐款数的中位数落在第____组;
(3)已知文华中学共有学生
1800人,请估算该校捐款数
不少于16元的学生人数.
如图,已知:点B、F、C、E在一条直线上,FB=CE,AC=DF。能否由上面的已知条件证明AB∥ED?如果能,请给出证明;如果不能,请从下列三个条件中选择一个合适的条件,添加到已知条件中,使AB∥ED成立,并给出证明。
供选择的三个条件(请从其中选择一个):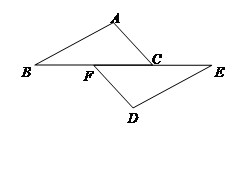
①AB=ED;
②BC=EF;
③∠ACB=∠DFE
如图,在方格纸上建立平面直角坐标系,线段AB的两个端点都在格点上,直线MN经过坐标原点,且点M的坐标是(1,2)。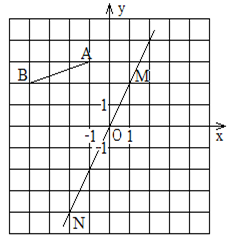
(1)写出点A、B的坐标;
(2)求直线MN所对应的函数关系式;
(3)作出线段AB关于直线MN的对称图形。