已知x=1是函数f(x)=mx3-3(m+1)x2+nx+1的一个极值点,其中m,n∈R.
(1)求m与n的关系式;
(2)求f(x)的单调区间;
(3)当x∈[-1,1]时,m<0,函数y=f(x)的图象上任意一点的切线斜率恒大于3m,求m的取值范围.
在平面直角坐标系 中,曲线
中,曲线 的参数方程为
的参数方程为 (
( ,
, 为参数),在以
为参数),在以 为极点,
为极点, 轴的正半轴为极轴的极坐标系中,曲线
轴的正半轴为极轴的极坐标系中,曲线 是圆心在极轴上,且经过极点的圆.已知曲线
是圆心在极轴上,且经过极点的圆.已知曲线 上的点
上的点 对应的参数
对应的参数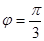 ,射线
,射线 与曲线
与曲线 交于点
交于点 ,
,
(1)求曲线 ,
, 的方程;
的方程;
(2)若点 ,
, 在曲线
在曲线 上,求
上,求 的值.
的值.
已知圆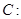
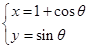 (
(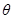 为参数)和直线
为参数)和直线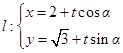 (其中为参数,
(其中为参数,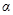 为直线的倾斜角),如果直线与圆
为直线的倾斜角),如果直线与圆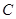 有公共点,求
有公共点,求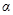 的取值范围.
的取值范围.
在平面直角坐标系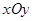 中,已知曲线
中,已知曲线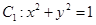 ,以平面直角坐标系
,以平面直角坐标系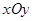 的原点
的原点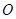 为极点,
为极点,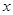 轴的正半轴为极轴,取相同的单位长度建立极坐标系,已知直线
轴的正半轴为极轴,取相同的单位长度建立极坐标系,已知直线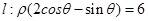 .
.
(1)将曲线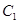 上的所有点的横坐标、纵坐标分别伸长为原来的
上的所有点的横坐标、纵坐标分别伸长为原来的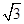 、
、 倍后得到曲线
倍后得到曲线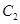 ,试写出直线的直角坐标方程和曲线
,试写出直线的直角坐标方程和曲线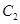 的参数方程;
的参数方程;
(2)在曲线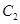 上求一点
上求一点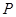 ,使点
,使点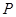 到直线的距离最大,并求出此最大值
到直线的距离最大,并求出此最大值
已知下列两个命题: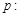 函数
函数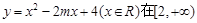 上单调递增;
上单调递增;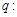 关于
关于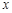 的不等式
的不等式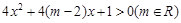 的解集为R,
的解集为R,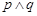 为假命题,
为假命题,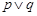 为真命题,求
为真命题,求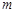 的取值范围。
的取值范围。
(本小题满分l2分)已知函数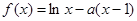 ,
,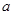 ∈R.
∈R.
(I)讨论函数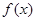 的单调性;
的单调性;
(Ⅱ)当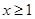 时,
时,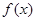 ≤
≤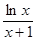 恒成立,求
恒成立,求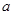 的取值范围.
的取值范围.