为了研究过山车的原理，某兴趣小组提出了下列设想：取一个与水平方向夹角为37°、长为l = 2.0m的粗糙倾斜轨道AB，通过水平轨道BC与竖直圆轨道相连，出口为水平轨道DE，整个轨道除 AB 段以外都是光滑的。其AB 与BC 轨道以微小圆弧相接，如图所示．一个小物块以初速度v0＝4.0m/s从某一高处水平抛出，到A点时速度方向恰好沿 AB 方向，并沿倾斜轨道滑下．已知物块与倾斜轨道的动摩擦因数 μ = 0.50．（g＝10m/s2、sin37°＝ 0.60、cos37° ＝0.80）
⑴求小物块到达A点时速度。
⑵要使小物块不离开轨道，并从轨道DE滑出，求竖直圆弧轨道的半径应该满足什么条件？
⑶为了让小物块不离开轨道，并且能够滑回倾斜轨道 AB，则竖直圆轨道的半径应该满足什么条件？
某升降电梯在下降时速度图象如图所示，一质量为60kg的人随电梯一起下降，g取10m/s2．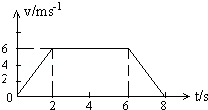
（1）电梯共下降了多大距离？
（2）人对电梯压力最大值、最小值各是多少？
如图所示，AB为固定在竖直平面内的
光滑圆弧轨道，轨道的B点与水平地面相切，其半径为R．质量为m的小球由A点静止释放，求：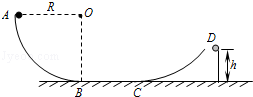
（1）小球滑到最低点B时，小球速度v的大小；
（2）小球刚到达最低点B时，轨道对小球支持力FN的大小；
（3）小球通过光滑的水平面BC滑上固定曲面，恰达最高点D，D到地面的高度为h（已知h＜R），则小球在曲面上克服摩擦力所做的功Wf．
在5m高处以10m/s的速度水平抛出一小球，不计空气阻力，g取10m/s2，求：
（1）小球在空中运动的时间；
（2）小球落地时的速度大小；
（3）小球落地点与抛出点之间的水平距离．
一质量m=10kg的物体静止在水平面上，在F=20N的水平恒力作用下开始运动．取g=l0m/s2，则：
（1）若水平面光滑，求物体的加速度大小；
（2）若水平面光滑，求物体2s末的速度大小；
（3）若水平面粗糙，且物体与水平面间的动摩擦因数μ=0.1，求物体的加速度大小．
如图甲所示，光滑绝缘水平面上，磁感应强度B=2T的匀强磁场以虚线MN为左边界，MN的左侧有一质量m=0.1kg，bc边长L1=0.2m，电阻R=2Ω的矩形线圈abcd．t=0时，用一恒定拉力F拉线圈，使其由静止开始向右做匀加速运动，经过时间1s，线圈的bc边到达磁场边界MN，此时立即将拉力F改为变力，又经过1s，线圈恰好完全进入磁场．整个运动过程中，线圈中感应电流i随时间t变化的图象如图乙所示．
（1）求线圈bc边刚进入磁场时的速度v1和线圈在第ls内运动的距离x；
（2）写出第2s内变力F随时间t变化的关系式；
（3）求出线圈ab边的长度L2．