设f(x)是定义在R上的奇函数,且当x≥0时,f(x)=x2,若对任意的x∈[t,t+2],不等式f(x+t)≥2f(x)恒成立,则实数t的取值范围是
| A．[√2,+∞) | B．[2,+∞) |
| C．(0,2] | D．[-√2,-1]∪[√2,0] |
下列函数中，在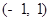
内有零点且单调递增的是( )
A． |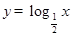
B． |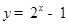
C． |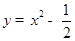
D． |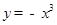
复数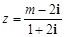
（
，
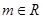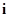是虚数单位）在复平面上对应的点不可能位于
| A．第一象限 | B．第二象限 | C．第三象限 | D．第四象限 |
集合M={a,b,c}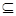
{—6，—5，—4，—2， 1，3，4}．若关于x 的不等式
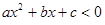恒有实数解，则满足条件的集合M 的个数是
| A．18 | B．22 | C．25 | D．27 |
已知向量a，b，c满足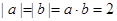
，
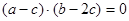，则
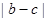的最小值为
A． |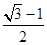
B． |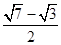
C． |
D． |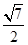
已知F1,F2是椭圆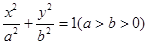
的左、右焦点，点P在椭圆上，且
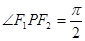记线段PF1与y轴的交点为Q，O为坐标原点，若△F1OQ与四边形OF2PQ的面积之比为1: 2，则该椭圆的离心率等于 ( )
A． |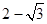
B． |
C． |
D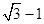． |