如图,已知直线l与抛物线x2=4y相切于点P(2,1),且与x轴交于点A,O为坐标原点,点B的坐标为(2,0),(1)若动点M满足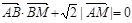 ,求点M的轨迹C;(2)若过点B的直线l′(斜率不等于零)与(1)中的轨迹C交于不同的两点E,F(E在B,F之间)试求△OBE与△OBF面积之比的取值范围.
,求点M的轨迹C;(2)若过点B的直线l′(斜率不等于零)与(1)中的轨迹C交于不同的两点E,F(E在B,F之间)试求△OBE与△OBF面积之比的取值范围.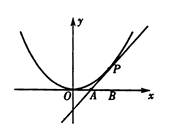
某班从6名班干部(其中男生4人,女生2人)中选3人参加学校学生会的干部竞选.
(1)设所选3人中女生人数为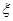 ,求
,求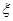 的分布列及数学期望;
的分布列及数学期望;
(2)在男生甲被选中的情况下,求女生乙也被选中的概率.
设数列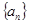 的前
的前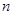 项和为
项和为 ,且
,且 …);
…);
①证明:数列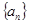 是等比数列;
是等比数列;
②若数列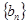 满足
满足 …),
…),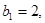 求数列
求数列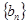 的通项公式。
的通项公式。
如图,海船甲位于岛屿A的南偏西60°方向的B处,且与岛屿A相距2海里,渔船乙以10海里/小时的速度从岛屿A出发沿正北方向航行,若渔船甲同时从B处出发沿北偏东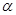 的方向追赶渔船乙,刚好用2小时追上。
的方向追赶渔船乙,刚好用2小时追上。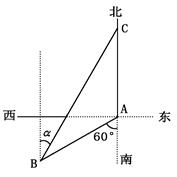
①求渔船甲的速度;
②求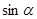 的值。
的值。
已知简单几何体的三视图如图所示
求该几何体的体积和表面积。
附:
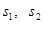 分别为上、下底面积
分别为上、下底面积
设等比数列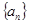 的前
的前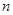 项和为
项和为 ,已知
,已知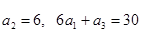 ,求
,求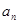 和
和 。
。