为了参加2011年国际铁人三项(游泳、自行车、长跑)系列赛业余组的比赛,李明针对自行车和长跑项目进行专项训练.某次训练中,李明骑自行车的平均速度为每分钟600米,跑步的平均速度为每分钟200米,自行车路段和长跑路段共5千米,用时15分钟.求自行车路段和长跑路段的长度.
在4×4的正方形方格中,△ABC和△DEF的顶点都在边长为1的小正方形的顶点上。填空:∠ABC=°,BC=.
判断△ABC与△DEF是否相似,并说明理由.

一天,小明和小玲玩纸片拼图游戏,发现利用图①中的三种材料各若干可以拼出一些长方形来解释某些等式。比如图②可以解释为:(a+2b)(a+b)=a2+3ab+2b2.图③可以解释为等式:
在虚线框中用图①中的基本图形拼成若干块(每种至少用一次)拼成一个矩形,使拼出的矩形面积为2a2+7ab+3b2,并标出此矩形的长和宽.
如图④,大正方形的边长为m,小正方形的边长为n,若用x、y表示四个矩形的两边长(x>y),观察图案,指出以下关系式
(1)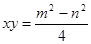 (2)
(2)
(3)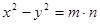 (4)
(4)
其中正确的有几个………………………………()
| A.1个 | B.2个 | C.3个 | D.4个 |

已知:如图,在△ABC中,∠B=40°,∠BCD=100°,EC平分∠ACB,
求:∠A与∠ACE的度数.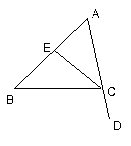
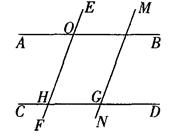
如图.已知AB∥CD,EF∥MN,且∠BOH=110°,求∠DHF和∠CGN的度数.
请你观察(1)中的结果,找出其中的规律,并用文字表述出来.
根据(2)中的结论,若两个角的两边分别平行,且其中一个角的度数是另一个角的2倍,求这两个角的度数.
观察下列等式,你会发现什么规律: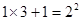
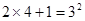
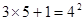
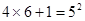
……
请将你发现的规律用仅含字母n(n为正整数)的等式表示出来,并说明它的正确性。