(本题满分15分)
已知各项均为正数的数列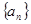 中,数列的前
中,数列的前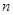 项和
项和 满足
满足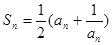 .
.
(1)求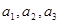 ;
;
(2)由(1)猜想数列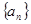 的通项公式,并用数学归纳法证明你的猜想.
的通项公式,并用数学归纳法证明你的猜想.
已知函数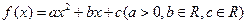 ,若函数
,若函数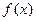 的最小值是
的最小值是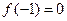 ,且
,且 ,对称轴是
,对称轴是 ,
,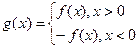 .
.
(1)求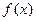 的解析式;
的解析式;
(2)求 的值;
的值;
(3)在(1)的条件下求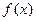 在区间
在区间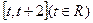 上的最小值.
上的最小值.
附加题(本大题共两个小题,每个小题10分,满分 20分,省级示范性高中要
把该题成绩计入总分,普通高中学生选作)
已知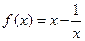 ,
,
(1)判断函数在区间(-∞,0)上的单调性,并用定义证明;
(2)画出该函数在定义域上的图像.(图像体现出函数性质即可)
(本题满分10分)
某租赁公司拥有汽车100辆,当每辆车的月租金为3000元时,可全部租出.当每辆车的月租金每增加50元时,未租出的车将会增加一辆.租出的车每月需维护费150元,未租出的车每月需维护费50元.
(1)当每辆车的月租金定为3600元时,能租出多少辆车?
(2)当每辆车的月租金定为多少元时,租赁公司的月收益最大?最大 月收益为多少?
月收益为多少?
(本题满分10分)
画出函数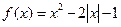 的图像,并写出该函数的单调区间与值域.
的图像,并写出该函数的单调区间与值域.
( 本题满分10分)
本题满分10分)
已知集合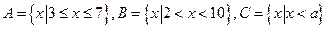 。
。
(1)求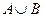 ;(2)求
;(2)求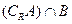 ;(3)若
;(3)若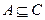 ,求a的取值范围.
,求a的取值范围.