(本小题满分12分)
函数 .
.
(Ⅰ)若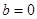 ,且
,且 在
在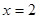 处取得极小值,求实数
处取得极小值,求实数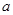 的值;
的值;
(Ⅱ)若函数 在
在 上是增函数,试探究
上是增函数,试探究 应满足什么条件;
应满足什么条件;
(Ⅲ)若 ,不等式
,不等式 对任意
对任意 恒成立,求整数
恒成立,求整数 的最大值.
的最大值.
已知函数 ,
,
(1)求 在x=1处的切线斜率的取值范围;
在x=1处的切线斜率的取值范围;
(2)求当 在x=1处的切线的斜率最小时,
在x=1处的切线的斜率最小时, 的解析式;
的解析式;
(3)在(Ⅱ)的条件下,是否总存在实数m,使得对任意的 ,总存在
,总存在 ,使得
,使得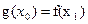 成立?若存在,求出实数m的取值范围;若不存在,说明理由.
成立?若存在,求出实数m的取值范围;若不存在,说明理由.
数列 的前
的前 项和为
项和为 ,数列
,数列 的前
的前 项的和为
项的和为 ,
, 为等差数列且各项均为正数,
为等差数列且各项均为正数, ,
,
 ,
,
(Ⅰ)求证:数列 是等比数列;
是等比数列;
(Ⅱ)若 ,
, ,
, 成等比数列,求
成等比数列,求 .
.
 如图,正方形
如图,正方形 和
和 的边长均为1,且它们所在平面互相垂直,
的边长均为1,且它们所在平面互相垂直, 为线段
为线段 的中点,
的中点, 为线段
为线段 的中点。
的中点。
(1)求证: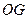 ∥面
∥面 ;
;
(2)求证:平面 ⊥平面
⊥平面 ;
;
(3)求直线 与平面
与平面 所成角的正切值.
所成角的正切值.
在 中,
中,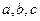 是角
是角 所对的边,已知
所对的边,已知 .
.
(Ⅰ)求角 的大小;
的大小;
(Ⅱ)若 的面积为
的面积为 ,求
,求 的值.
的值.
O为坐标原点,  和
和 两点分别在射线
两点分别在射线
 上移动,且
上移动,且 ,动点P满足
,动点P满足 ,
,
记点P的轨迹为C.
(I)求 的值;
的值;
(II)求P点的轨迹C的方程,并说明它表示怎样的曲线?
(III)设点G(-1,0),若直线 与曲线C交于M、N两点,且M、N两点都在以G为圆心的圆上,求
与曲线C交于M、N两点,且M、N两点都在以G为圆心的圆上,求 的取值范围.
的取值范围.