已知函数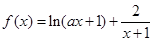 ,其中
,其中 .
.
(1)若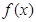 在
在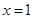 处取得极值,求曲线
处取得极值,求曲线 在点
在点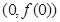 处的切线方程;
处的切线方程;
(2)讨论函数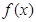 在
在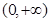 的单调性;
的单调性;
(3)若函数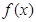 在
在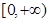 上的最小值为2,求
上的最小值为2,求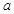 的取值范围.
的取值范围.
如图,是一个奖杯的三视图(单位:cm),底座是正四棱台.
(1)求这个奖杯的体积;
(2)求这个奖杯底座的侧面积.
已知直线l1:x+my+6=0(m≠0),直线l2:(m-2)x+3y+2m=0,
求m的值, 使得l1和l2 (1) 平行 (2) 垂直
已知动点P与双曲线x2-y2=1的两个焦点F1,F2的距离之和为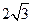 定值,
定值,
(1)求动点P的轨迹方程;
(2)设M(0,-1),若斜率为k(k≠0)的直线l与P点的轨迹交于不同的两点A、B,若要使|MA|=|MB|,试求k的取值范围.
设F1、F2分别为椭圆C: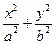 =1(a>b>0)的左、右焦点,过F2的直线l与椭圆C相交于A,B两点,直线l的倾斜角为60°,F1到直线l的距离为2
=1(a>b>0)的左、右焦点,过F2的直线l与椭圆C相交于A,B两点,直线l的倾斜角为60°,F1到直线l的距离为2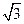 .
.
(1)求椭圆C的焦距;
(2)如果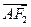 =2
=2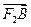 ,求椭圆C的方程.
,求椭圆C的方程.
在平面直角坐标系xOy中,直线l过抛物线y2=4x的焦点F交抛物线于A、B两点.
(1) 若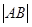 =8,求直线l的斜率
=8,求直线l的斜率
(2)若 =m,
=m,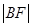 =n.求证
=n.求证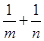 为定值
为定值