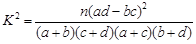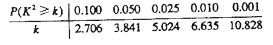如图,在底面是正方形的四棱锥P—ABCD中,平面PCD⊥平面ABCD,PC=PD=CD=2.
(I)求证:PD⊥BC;
(II)求二面角B—PD—C的正切值。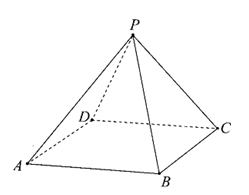
已知一扇形的圆心角为 ,所在圆的半径为R,若扇形的周长为40cm,当它的圆心角
,所在圆的半径为R,若扇形的周长为40cm,当它的圆心角 为多少弧度时,该扇形的面积最大?最大面积为多少?
为多少弧度时,该扇形的面积最大?最大面积为多少?
如图,已知AD是△ABC的外角∠EAC的平分线,交BC的延长线于点D,延长DA交△ABC的外接圆于点F,连接FB、FC.
(1)求证:FB=FC;
(2)求证:FB2=FA·FD;
(3)若AB是△ABC外接圆的直径,∠EAC=120°,BC=6 cm,求AD的长.
设函数 的图象如图所示,且与
的图象如图所示,且与 在原点相切,若函数的极小值为
在原点相切,若函数的极小值为 ,(1)求
,(1)求 的值;(2)求函数的递减区间.
的值;(2)求函数的递减区间.
如图,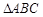 的角平分线
的角平分线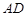 的延长线交它的外接圆于点
的延长线交它的外接圆于点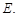
(Ⅰ)证明: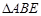 ∽△
∽△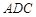 ;
;
(Ⅱ)若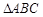 的面积
的面积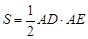 ,求
,求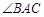 的大小.
的大小.
某企业有两个分厂生产某种零件,按规定内径尺寸(单位:mm)的值落在[29.94,30.06)的零件为优质品.从两个分厂生产的零件中各抽出500件,量其内径尺寸,的结果如下表:
甲厂:
乙厂:
(1)试分别估计两个分厂生产的零件的优质品率;
(2)由以上统计数据填下面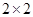 列联表,并问是否有99%的把握认为“两个分厂生产的零件的质量有差异”.
列联表,并问是否有99%的把握认为“两个分厂生产的零件的质量有差异”.
| 甲 厂 |
乙 厂 |
合计 |
|
| 优质品 |
|||
| 非优质品 |
|||
| 合计 |
附: