某校从参加某次知识竞赛的同学中，选取60名同学将其成绩（百分制）（均为整数）分成6组后，得到部分频率分布直方图（如图），观察图形中的信息，回答下列问题.
（Ⅰ）求分数在[70,80）内的频率，并补全这个频率分布直方图；
（Ⅱ）从频率分布直方图中，估计本次考试的平均分；
（Ⅲ）若从60名学生中随机抽取2人，抽到的学生成绩在[40,70）记0分，在[70,100]记1分，用X表示抽取结束后的总记分，求X的分布列和数学期望.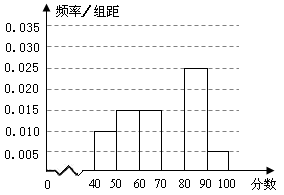
（本小题满分16分）
已知函数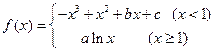
的图象过点
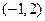，且在点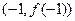
处的切线与直线
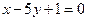垂直．
(1) 求实数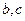
的值；(6分)
(2) 求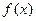
在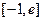
（
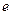为自然对数的底数）上的最大值；(5分)
(3) 对任意给定的正实数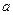
，曲线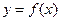
上是否存在两点
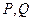，使得
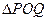是以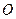
为直角顶点的直角三角形，且此三角形斜边中点在
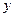轴上？(5分)
（本小题满分16分）
两县城A和B相距20km，现计划在两县城外以AB为直径的半圆弧
上选择一点C建造垃圾处理厂，其对城市的影响度与所选地点到城市的的距离有关，对城A和城B的总影响度为城A与城B的影响度之和，记C点到城A的距离为x km，建在C处的垃圾处理厂对城A和城B的总影响度为y,统计调查表明：垃圾处理厂对城A的影响度与所选地点到城A的距离的平方成反比，比例系数为4；对城B的影响度与所选地点到城B的距离的平方成反比，比例系数为k ,当垃圾处理厂建在的中点时，对城A和城B的总影响度为0.065.
（1）按下列要求建立函数关系式：
（i）设
（rad），将
表示成
的函数；并写出函数的定义域. (5分)
（ii）设
（km），将表示成
的函数；并写出函数的定义域.(5分)
（2）请你选用（1）中的一个函数关系确定垃圾处理厂的位置，使建在此处的垃圾处理厂对城A和城B的总影响度最小？(6分)
(本题满分15分)
已知数列{an}的前n项和为Sn，且a1=1，Sn=n2an（n∈N*）.
（1）试求出S1，S2，S3，S4，并猜想Sn的表达式；
（2）用数学纳法证明你的猜想，并求出an的表达式.
(本题满分15分)
已知a、b∈（0，+∞），且a+b=1,
求证：(1) ab≤
(2)
+
≥8; (3) 
+ 
≥
. (5分+5分+5分)
（本小题满分14分）
已知
p：
，q：
．
⑴ 若p是q充分不必要条件，求实数
的取值范围；
⑵若“非p”是“非q”的充分不必要条件，求实数的取值范围．