在平面直角坐标系xOy中，已知点A(-1, 0)、B(1, 0), 动点C满足条件：△ABC的周长为2＋2.记动点C的轨迹为曲线W.
(Ⅰ)求W的方程；
(Ⅱ)经过点（0, ）且斜率为k的直线l与曲线W有两个不同的交点P和Q，
求k的取值范围；
（Ⅲ）已知点M（，0），N（0, 1），在(Ⅱ)的条件下，是否存在常数k，使得向量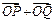
与
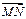共线？如果存在，求出k的值；如果不存在，请说明理由.
试比较nn+1与（n+1）n（n∈N*）的大小．
当n=1时，有nn+1（n+1）n（填＞、=或＜）；
当n=2时，有nn+1（n+1）n（填＞、=或＜）；
当n=3时，有nn+1（n+1）n（填＞、=或＜）；
当n=4时，有nn+1（n+1）n（填＞、=或＜）；
猜想一个一般性的结论，并加以证明．
已知数列{an}的各项都是正数，且满足：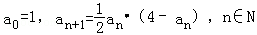
．
（1）求a1，a2；
（2）证明an＜an+1＜2，n∈N．
用数学归纳法证明不等式：
+
+
+…+
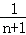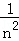＞1（n∈N*且n＞1）．
证明不等式
（n∈N*）
已知函数f（x）=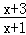
（x≠﹣1）．设数列{an}满足a1=1，an+1=f（an），数列{bn}满足bn=|an﹣
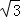|，Sn=b1+b2+…+bn（n∈N*）．
（Ⅰ）用数学归纳法证明bn≤
；
（Ⅱ）证明Sn＜
．