已知椭圆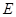 的中心在原点,焦点在
的中心在原点,焦点在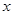 轴上,椭圆上的点到焦点的最小距离为
轴上,椭圆上的点到焦点的最小距离为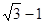 ,离心率
,离心率 .
.
(1)求椭圆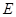 的方程;
的方程;
(2)若直线 交
交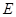 于
于 、
、 两点,点
两点,点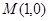 ,问是否存在
,问是否存在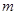 ,使
,使 ?若存在求出
?若存在求出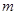 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
已知离心率为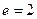 的双曲线
的双曲线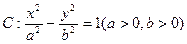 ,双曲线
,双曲线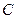 的一个焦点到
的一个焦点到
渐近线的距离是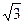
(1)求双曲线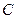 的方程
的方程
(2)过点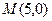 的
的 直线
直线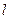 与双曲线
与双曲线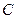 交于
交于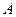 、
、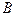 两点,交
两点,交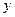 轴于
轴于 点
点 ,当
,当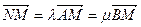 ,且
,且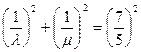 时,求直线
时,求直线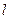 的方程
的方程
(
如图,在五面体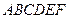 中,
中,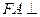 平面
平面 ,
,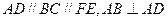 ,
,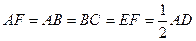
(1)求异面直线 和
和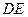 所成的角
所成的角
(2)求二面角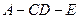 的大小
的大小
(3)若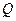 为
为 的中点,
的中点,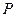 为
为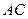 上一点,当
上一点,当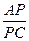 为何值时,
为何值时,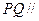 平面
平面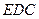 ?
?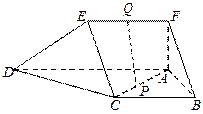
(
某篮球联赛的总决赛在甲、乙两队之间角逐。采用七场四胜制,即有一队胜四场,则此队获胜,
同时比赛结束。在每场比赛中,两队获胜的概率相等。根据以往资料统计,每场比赛组织者可获
门票收入32万元,两队决出胜负后,问:
(1)组织者在此次决赛中,获门票收入为128万元的概率是多少?
(2)设组织者在此次决赛中获门票收入为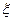 ,求
,求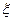 的分布列及
的分布列及 。
。
已知椭圆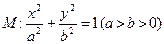 的离心率为
的离心率为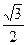 ,短轴的长为2.
,短轴的长为2.
(1)求椭圆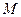 的标准方程
的标准方程
(2)若经过点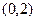 的直线
的直线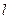 与椭圆
与椭圆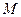 交于
交于 两点,满足
两点,满足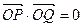 ,求
,求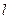 的方程
的方程
袋中装有黑球和白球共7个,从中任取2个球都是白球的概率为 .现在甲、乙两人从袋中轮流摸取1球,甲先取,乙后取,然后甲再取……取后不放回,直到两人中有一人取到白球时即终止,每个球在每一次被取出的机会是等可能的.
.现在甲、乙两人从袋中轮流摸取1球,甲先取,乙后取,然后甲再取……取后不放回,直到两人中有一人取到白球时即终止,每个球在每一次被取出的机会是等可能的.
(1)求袋中原有白球的个数;
(2)求取球两次终止的概率
(3)求甲取到白球的概率